Rhythms and alternating patterns in plants as emergent properties of a model of interaction between development and functioning

Abstract

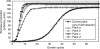
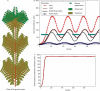
Background and aims: To model plasticity of plants in their environment, a new version of the functional-structural model GREENLAB has been developed with full interactions between architecture and functioning. Emergent properties of this model were revealed by simulations, in particular the automatic generation of rhythms in plant development. Such behaviour can be observed in natural phenomena such as the appearance of fruit (cucumber or capsicum plants, for example) or branch formation in trees.

Methods: In the model, a single variable, the source-sink ratio controls different events in plant architecture. In particular, the number of fruits and branch formation are determined as increasing functions of this ratio. For some sets of well-chosen parameters of the model, the dynamical evolution of the ratio during plant growth generates rhythms.

Key results and conclusions: Cyclic patterns in branch formation or fruit appearance emerge without being forced by the model. The model is based on the theory of discrete dynamical systems. The mathematical formalism helps us to explain rhythm generation and to control the behaviour of the system. Rhythms can appear during both the exponential and stabilized phases of growth, but the causes are different as shown by an analytical study of the system. Simulated plant behaviours are very close to those observed on real plants. With a small number of parameters, the model gives very interesting results from a qualitative point of view. It will soon be subjected to experimental data to estimate the model parameters.

Fig. 1.

Description of the GREENLAB growth cycle: blossoming of buds leads to appearance of organs in the plant. Each leaf is a source that produces biomass depending on the environmental conditions. It results in an incremental reserve pool available to all growing organs (leaves, internodes) and buds. The biomass allocated to buds is used for the construction of the preformed organs when they appear.

Fig. 2.

Appearance of rhythm in the branching system of a Leeuwenberg architectural model (Hallé et al., 1978). The plant (A) and its topology (B) are shown. On each metamer, two axillary buds are activated according to the rate of growth demand satisfaction. Parameters are A = 3·18 × 10⁻⁵, B = 0·11, C = 10. The simulation only presents the exponential phase of growth as shown by the graph of biomass production (D). The production limit is 674·04. It is observed that the ratio of available biomass to demand (C) has a periodic evolution: when it exceeds a threshold (with a value of 0·01), two branches are formed on each metamer, which multiplies the demand by two and decreases in proportion the rate of growth demand satisfaction (D).

Fig. 3.

Influence of the threshold value of the rate of growth demand satisfaction for appearance of fruit. The behaviours of monocaulus plants are compared with the same entry parameters of the model (A = 3·53 × 10⁻⁴, B = 6·67 × 10⁻², p_e = 0·5, p_a = 1, e = 0·025). But fruit appearance is more or less sensitive to the ratio of available biomass to demand. Plants a, b, c and d have, respectively, threshold values of 1, 2, 3 and 4. The lower the threshold is, the more fruits the plant produces and the smaller it is. It is observed that plant d grows much faster at the beginning, before the appearance of fruit. When fruits start to appear, the rate of growth demand satisfaction oscillates around the threshold (B), and rhythms in fructification are observed with different patterns for plants a, b, c and d (A).

Fig. 4.

Biomass production for monocaulus plants with fruit appearance depending on the rate of growth demand satisfaction. The behaviours of the monocaulus trees shown in Fig. 3 are compared. Plants a, b, c and d have, respectively, threshold values of 1, 2, 3 and 4. A control plant with a threshold value of 0 is added. It has the same limit behaviour as plant a (production of one new fruit at each growth cycle) but grows much slower at the beginning because it is influenced by early fruit appearance. In both cases, C = 38·2 can be computed, which gives Q_∞ = 169·35. More generally, biomass production tends to stabilize, and it converges at 188·5 for plants c and d. Slight oscillations around the limit value for plant b are observed since the number of fruits in the plant is not constant.

Fig. 5.

Branched plant with branch appearance depending on the rate of growth demand satisfaction. Parameters are A = 3·53 × 10⁻⁴, B = 6·67 × 10⁻², b₂ = 1, p_a = 1, p_e = 0·5, p_c = 1, t_a = 15, t_e = 10 and branches remain alive for ten growth cycles. In (C), it is observed that the biomass production stabilizes (see eqn 1). The demand of the different organs varies according to their numbers (see B), leading to oscillations in the ratio of available biomass to demand and rhythm in branch formation (A). It is noticed that, except for the exponential phase, branches appear when demand is below a value depending on the threshold value of branch appearance (B) and biomass production tends to be 188·5 (C).

Fig. 6.

Plant with fruit and branch appearances depending on the rate of growth demand satisfaction. Parameters are A = 3·53 × 10⁻⁴, B = 6·67 × 10⁻², β₂ = 1, p_a = 1, p_e = 0·5, p_c = 1, t_a = 15 and t_e = 10, and branches remain alive during ten growth cycles. To simplify the representation of a tree, leaves are not drawn (A). Rhythms appear both in fruit production and branch appearance. The evolution of the demand is quite complex, combining both processes with different costs (B). Fruit appearance is more frequent than branch appearance since it is triggered by a lower rate of growth demand satisfaction. Biomass production oscillates around 187·5 (C) and could be analytically computed by a method described in Grange (2006).