Simulation of Ca2+ movements within the sarcomere of fast-twitch mouse fibers stimulated by action potentials
- PMID: 17724162
- PMCID: PMC2151645
- DOI: 10.1085/jgp.200709827
Simulation of Ca2+ movements within the sarcomere of fast-twitch mouse fibers stimulated by action potentials
Abstract
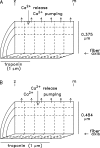
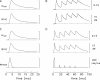
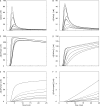
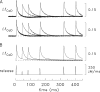
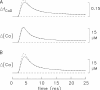
Ca(2+) release from the sarcoplasmic reticulum (SR) of skeletal muscle takes place at the triadic junctions; following release, Ca(2+) spreads within the sarcomere by diffusion. Here, we report multicompartment simulations of changes in sarcomeric Ca(2+) evoked by action potentials (APs) in fast-twitch fibers of adult mice. The simulations include Ca(2+) complexation reactions with ATP, troponin, parvalbumin, and the SR Ca(2+) pump, as well as Ca(2+) transport by the pump. Results are compared with spatially averaged Ca(2+) transients measured in mouse fibers with furaptra, a low-affinity, rapidly responding Ca(2+) indicator. The furaptra Deltaf(CaD) signal (change in the fraction of the indicator in the Ca(2+)-bound form) evoked by one AP is well simulated under the assumption that SR Ca(2+) release has a peak of 200-225 microM/ms and a FDHM of approximately 1.6 ms (16 degrees C). Deltaf(CaD) elicited by a five-shock, 67-Hz train of APs is well simulated under the assumption that in response to APs 2-5, Ca(2+) release decreases progressively from 0.25 to 0.15 times that elicited by the first AP, a reduction likely due to Ca(2+) inactivation of Ca(2+) release. Recovery from inactivation was studied with a two-AP protocol; the amplitude of the second release recovered to >0.9 times that of the first with a rate constant of 7 s(-1). An obvious feature of Deltaf(CaD) during a five-shock train is a progressive decline in the rate of decay from the individual peaks of Deltaf(CaD). According to the simulations, this decline is due to a reduction in available Ca(2+) binding sites on troponin and parvalbumin. The effects of sarcomere length, the location of the triadic junctions, resting [Ca(2+)], the parvalbumin concentration, and possible uptake of Ca(2+) by mitochondria were also investigated. Overall, the simulations indicate that this reaction-diffusion model, which was originally developed for Ca(2+) sparks in frog fibers, works well when adapted to mouse fast-twitch fibers stimulated by APs.
Figures
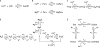







Similar articles
-
Calcium indicators and calcium signalling in skeletal muscle fibres during excitation-contraction coupling.Prog Biophys Mol Biol. 2011 May;105(3):162-79. doi: 10.1016/j.pbiomolbio.2010.06.001. Epub 2010 Jun 25. Prog Biophys Mol Biol. 2011. PMID: 20599552 Free PMC article. Review.
-
Intracellular calcium movements during excitation-contraction coupling in mammalian slow-twitch and fast-twitch muscle fibers.J Gen Physiol. 2012 Apr;139(4):261-72. doi: 10.1085/jgp.201210773. J Gen Physiol. 2012. PMID: 22450485 Free PMC article. Review.
-
Comparison of myoplasmic calcium movements during excitation-contraction coupling in frog twitch and mouse fast-twitch muscle fibers.J Gen Physiol. 2013 May;141(5):567-83. doi: 10.1085/jgp.201310961. J Gen Physiol. 2013. PMID: 23630340 Free PMC article.
-
Sarcoplasmic reticulum calcium release compared in slow-twitch and fast-twitch fibres of mouse muscle.J Physiol. 2003 Aug 15;551(Pt 1):125-38. doi: 10.1113/jphysiol.2003.041608. Epub 2003 Jun 17. J Physiol. 2003. PMID: 12813151 Free PMC article.
-
Measurement and simulation of myoplasmic calcium transients in mouse slow-twitch muscle fibres.J Physiol. 2012 Feb 1;590(3):575-94. doi: 10.1113/jphysiol.2011.220780. Epub 2011 Nov 28. J Physiol. 2012. PMID: 22124146 Free PMC article.
Cited by
-
Multiple genetic loci define Ca++ utilization by bloodstream malaria parasites.BMC Genomics. 2019 Jan 16;20(1):47. doi: 10.1186/s12864-018-5418-y. BMC Genomics. 2019. PMID: 30651090 Free PMC article.
-
Numerous Trigger-like Interactions of Kinases/Protein Phosphatases in Human Skeletal Muscles Can Underlie Transient Processes in Activation of Signaling Pathways during Exercise.Int J Mol Sci. 2023 Jul 7;24(13):11223. doi: 10.3390/ijms241311223. Int J Mol Sci. 2023. PMID: 37446402 Free PMC article. Review.
-
Calcium indicators and calcium signalling in skeletal muscle fibres during excitation-contraction coupling.Prog Biophys Mol Biol. 2011 May;105(3):162-79. doi: 10.1016/j.pbiomolbio.2010.06.001. Epub 2010 Jun 25. Prog Biophys Mol Biol. 2011. PMID: 20599552 Free PMC article. Review.
-
Intracellular calcium movements during excitation-contraction coupling in mammalian slow-twitch and fast-twitch muscle fibers.J Gen Physiol. 2012 Apr;139(4):261-72. doi: 10.1085/jgp.201210773. J Gen Physiol. 2012. PMID: 22450485 Free PMC article. Review.
-
Cytosolic Ca2+ gradients and mitochondrial Ca2+ uptake in resting muscle fibers: A model analysis.Biophys Rep (N Y). 2023 Jul 17;3(3):100117. doi: 10.1016/j.bpr.2023.100117. eCollection 2023 Sep 13. Biophys Rep (N Y). 2023. PMID: 37576797 Free PMC article.
References
-
- Brown, I.E., D.H. Kim, and G.E. Loeb. 1998. The effect of sarcomere length on triad location in intact feline caudofemoralis muscle fibres. J. Muscle Res. Cell Motil. 19:473–477. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

