Evidence for the flexible sensorimotor strategies predicted by optimal feedback control
- PMID: 17728449
- PMCID: PMC6673117
- DOI: 10.1523/JNEUROSCI.1110-06.2007
Evidence for the flexible sensorimotor strategies predicted by optimal feedback control
Abstract
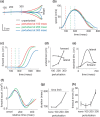
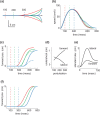
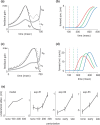
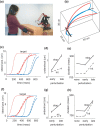
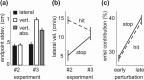
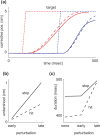
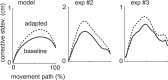
Everyday movements pursue diverse and often conflicting mixtures of task goals, requiring sensorimotor strategies customized for the task at hand. Such customization is mostly ignored by traditional theories emphasizing movement geometry and servo control. In contrast, the relationship between the task and the strategy most suitable for accomplishing it lies at the core of our optimal feedback control theory of coordination. Here, we show that the predicted sensitivity to task goals affords natural explanations to a number of novel psychophysical findings. Our point of departure is the little-known fact that corrections for target perturbations introduced late in a reaching movement are incomplete. We show that this is not simply attributable to lack of time, in contradiction with alternative models and, somewhat paradoxically, in agreement with our model. Analysis of optimal feedback gains reveals that the effect is partly attributable to a previously unknown trade-off between stability and accuracy. This yields a testable prediction: if stability requirements are decreased, then accuracy should increase. We confirm the prediction experimentally in three-dimensional obstacle avoidance and interception tasks in which subjects hit a robotic target with programmable impedance. In additional agreement with the theory, we find that subjects do not rely on rigid control strategies but instead exploit every opportunity for increased performance. The modeling methodology needed to capture this extra flexibility is more general than the linear-quadratic methods we used previously. The results suggest that the remarkable flexibility of motor behavior arises from sensorimotor control laws optimized for composite cost functions.
Figures

References
-
- Anderson F, Pandy M. Dynamic optimization of human walking. J Biomech Eng. 2001;123:381–390. - PubMed
-
- Bernstein N. Oxford: Pergamon; 1967. The coordination and regulation of movements.
-
- Bertsekas D. Ed 2. Bellmont, MA: Athena Scientific; 2001. Dynamic programming and optimal control.
-
- Bizzi E, Hogan N, Mussa-Ivaldi F, Giszter S. Does the nervous system use equilibrium-point control to guide single and multiple joint movements? Behav Brain Sci. 1992;15:603–613. - PubMed
-
- Burdet E, Osu R, Franklin D, Milner T, Kawato M. The central nervous system stabilizes unstable dynamics by learning optimal impedance. Nature. 2001;414:446–449. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
