Generalization of distance to higher dimensional objects

Abstract

The measurement of distance between two objects is generalized to the case where the objects are no longer points but are one-dimensional. Additional concepts such as nonextensibility, curvature constraints, and noncrossing become central to the notion of distance. Analytical and numerical results are given for some specific examples, and applications to biopolymers are discussed.

Fig. 1.

Three representative pairs of curves. (A) Straight line curve rotated by π/2. (B) One string has a finite radius of curvature, the other is straight. (C) A canonical example where noncrossing is important; the curves are displaced for easy visualization but should be imagined to be superimposed.

Fig. 2.

The minimal transformation from A to B in Fig. 1A involves the propagation of a kink along curve B. The end point of the curve at intermediate states satisfies x + y = L, the equation for a straight line. A similar linear equation holds for any point on the curve; thus, no solution with shorter distance can exist. An intermediate configuration is shown in red. Alternative transformations are possible with kinks along A as well as multiple kinks (see text).

Fig. 3.

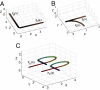
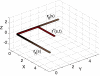
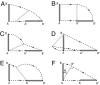
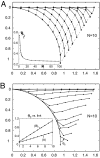
Transformations between two rigid rods. A undergoes simultaneous translation and rotation and so is not extremal. B is extremal and minimal. The rod cannot rotate any less given that it translates first. However, this transformation is a weak or local minimum. C–E are extremal in bulk but not minimal because they violate corner conditions (A. Mohazab and S.S.P., unpublished data). F is the global minimum. It rotates the minimal amount, and both A and B move monotonically toward A′, B′. A purely straight-line transformation exists but involves moving point A away from A′ before moving toward it (similar to D), thus covering a larger distance than the minimal transformation.

Fig. 4.

Two minimal transformations between the curves shown in Fig. 1B, for N = 10 links. (A) The global minimal transformation r*(s, t), with * ≈ 0.330 L². (B) A local minimum with ≈ 0.335 L². In A, links with one end touching curve r_B rotate; the others translate first from r_A, rotating only when one end of a link has touched r_B. In B, they rotate first from r_A and then translate into r_B. Dashed lines in A show the paths travelled for each bead. (A Inset) The total distance travelled as a function of the number of links N, with various N plotted as filled circles to indicate the rapid decrease and asymptotic limit to _∞ ≈ 0.251 L². (B Inset) The minimal angle each link must rotate during the transformation; it is less for the transformation in A. Animations of these transformations are provided as supporting information (SI) Movies 1–4.