Susceptible-infected-recovered epidemics in dynamic contact networks

Abstract

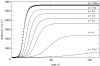
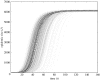
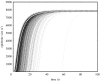
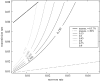
Contact patterns in populations fundamentally influence the spread of infectious diseases. Current mathematical methods for epidemiological forecasting on networks largely assume that contacts between individuals are fixed, at least for the duration of an outbreak. In reality, contact patterns may be quite fluid, with individuals frequently making and breaking social or sexual relationships. Here, we develop a mathematical approach to predicting disease transmission on dynamic networks in which each individual has a characteristic behaviour (typical contact number), but the identities of their contacts change in time. We show that dynamic contact patterns shape epidemiological dynamics in ways that cannot be adequately captured in static network models or mass-action models. Our new model interpolates smoothly between static network models and mass-action models using a mixing parameter, thereby providing a bridge between disparate classes of epidemiological models. Using epidemiological and sexual contact data from an Atlanta high school, we demonstrate the application of this method for forecasting and controlling sexually transmitted disease outbreaks.

Figure 1

Trajectories of the NE model (solid lines, table 4) are compared for several values of the mixing rate (ρ) with an analogous mass-action model (circles, equations (2.22) and (2.23)). The degree distribution is Poisson (z=1.5) and r=μ=0.2.

Figure 2

One-thousand stochastic simulations (small dots) are compared with the predicted trajectory of a NE epidemic (large dots) in a Poisson network (z=1.5). r=0.2, μ=0.1 and ρ=0.25.

Figure 3

One-thousand stochastic simulations (small dots) are compared with the predicted trajectory of a NE epidemic (large dots) in a power-law network (α=2.1, κ=75). r=0.2, μ=0.1 and ρ=0.20.

Figure 4

The final epidemic size as predicted by the NE model (table 4) is shown with respect to the transmission rate r and recovery rate μ for the Atlanta syphilis data. Contours are also provided for τ=0.637 and 0.20.