Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Editorial
. 2007:3:137.
doi: 10.1038/msb4100179. Epub 2007 Sep 18.

Towards a theory of biological robustness

Hiroaki Kitano
Editorial

Towards a theory of biological robustness

Hiroaki Kitano. Mol Syst Biol. 2007.
No abstract available

PubMed Disclaimer

Figures

Figure 1
Figure 1
Fundamental principles, structural principles, and design. Living organisms are designed through evolution and perturbed under environmental constraints. Each instance of design is an actual life form that exists in the past, present, and future. Viable design is only possible within the constraints of fundamental principles and structural principles. Fundamental principles include basic laws such as quantum theory, Maxwell's equations, basic chemistry, and physics that apply to almost everything universally. Structural principles govern properties of systems and have a specific architecture such as control theory, communication theory, and various principles applied to specific configurations of components that are generally architecture-specific and context-dependent. For systems biology to be truly successful, not only studies on specific instances of life, but also studies on principles governing the entire design space are required.
Figure 2
Figure 2
Stability, homeostasis, and robustness. Assume that the initial state of the system is at the center of steady state 1. A perturbation may drive the state of the system toward the boundary of the basin of attractor of steady state 1. When the state of the system returns to its original state, it is called ‘stability' and ‘homeostasis'. When it transits to steady state 2, stability is once lost and the system regains its stability in the new steady state. If the system's functions are still intact, such transition of state is considered a part of robust response. The system is considered to be robust if it maintains functions regardless of whether it is in steady state 1 or 2. On extreme case, the system may continue to transit between multiple steady state points to cope with perturbations.
Figure 3
Figure 3
Robustness. Perturbations are imposed on each feature and at different degree if applicable. The figure illustrate coarse grain view of perturbation space where there are six features to be perturbed each of which is perturbed at six different degree. Colors on box for each perturbation indicate how system responded to each perturbation. Red box indicate that system fail to maintain its function. Different blue colors show the level of degradation of the function. Although the area the function is maintained is same in (A and B), (A) is considered more robust as the function is better preserved than (B).
Figure 4
Figure 4
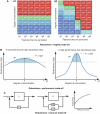
Robustness trade-offs. (A) If robustness is strictly conserved, then any increase in robustness for specific perturbation shall be compensated by increase in fragility elsewhere. Left panel is a profile of robustness of a hypothetical system that responds equally to perturbations of each feature (from g1 to g6). Now, if the system is tuned to cope better with perturbations of a subset of features (g1, g2, and g3), then robustness against other subset of perturbations are significantly reduced (right panel). Total robustness of both systems over this perturbation space remains equal. (B) If the robustness-performance trade-off holds, a system that is tuned to attain high performance might be less robust than a system with moderate performance but a higher level of robustness. Let's assume Ya=fa(0) for system A where f(0) is the performance of the function of the system under perturbation ‘0' (no perturbation) and Ra is the robustness of the system over some defined perturbations. Although the figure simply refers to the colored areas for ease of understanding, the exact Ra needs to be calibrated based on Equation (1). The horizontal dashed lines indicate the threshold under which the system fails to perform the function considered. A robustness-performance trade-off would then imply that YaRa=YbRb. (C) Identical circuits with slightly difference resource use are shown. Both use NFB loop, but one uses only one resistor in the loop, whereas the other one uses two resistors in parallel. Parallel use of components significantly improves robustness of the system against component failure, but requires more resources. Here, the probability of degradation of system function can be computed using basic equations from reliability engineering so that the difference of robustness can be derived for simple example like this one. It is however challenging to derive an expression for more complex systems under various perturbations. The question is how can we compute formula image where mS1 and mS2 are resource used for system S1 and S2, respectively. The function U would relate the difference of resource use to the difference in robustness as a function of some design principles according to which resources are used. Whether it is at all possible to define such a function and, more fundamentally, whether such conservation actually exists, in either relative or strict manner, remains open.
See this image and copyright information in PMC

References

    1. Alon U, Surette MG, Barkai N, Leibler S (1999) Robustness in bacterial chemotaxis. Nature 397: 168–171 - PubMed
    1. Baisse B, Bouzourene H, Saraga EP, Bosman FT, Benhattar J (2001) Intratumor genetic heterogeneity in advanced human colorectal adenocarcinoma. Int J Cancer 93: 346–352 - PubMed
    1. Balaban NQ, Merrin J, Chait R, Kowalik L, Leibler S (2004) Bacterial persistence as a phenotypic switch. Science 305: 1622–1625 - PubMed
    1. Barkai N, Leibler S (1997) Robustness in simple biochemical networks. Nature 387: 913–917 - PubMed
    1. Bhalla US, Iyengar R (2001) Robustness of the bistable behavior of a biological signaling feedback loop. Chaos 11: 221–226 - PubMed

Publication types