Developing a spatial-statistical model and map of historical malaria prevalence in Botswana using a staged variable selection procedure

Abstract

Background: Several malaria risk maps have been developed in recent years, many from the prevalence of infection data collated by the MARA (Mapping Malaria Risk in Africa) project, and using various environmental data sets as predictors. Variable selection is a major obstacle due to analytical problems caused by over-fitting, confounding and non-independence in the data. Testing and comparing every combination of explanatory variables in a Bayesian spatial framework remains unfeasible for most researchers. The aim of this study was to develop a malaria risk map using a systematic and practicable variable selection process for spatial analysis and mapping of historical malaria risk in Botswana.

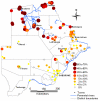
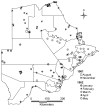
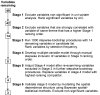
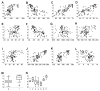
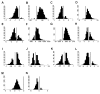
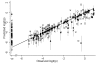
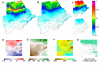
Results: Of 50 potential explanatory variables from eight environmental data themes, 42 were significantly associated with malaria prevalence in univariate logistic regression and were ranked by the Akaike Information Criterion. Those correlated with higher-ranking relatives of the same environmental theme, were temporarily excluded. The remaining 14 candidates were ranked by selection frequency after running automated step-wise selection procedures on 1000 bootstrap samples drawn from the data. A non-spatial multiple-variable model was developed through step-wise inclusion in order of selection frequency. Previously excluded variables were then re-evaluated for inclusion, using further step-wise bootstrap procedures, resulting in the exclusion of another variable. Finally a Bayesian geo-statistical model using Markov Chain Monte Carlo simulation was fitted to the data, resulting in a final model of three predictor variables, namely summer rainfall, mean annual temperature and altitude. Each was independently and significantly associated with malaria prevalence after allowing for spatial correlation. This model was used to predict malaria prevalence at unobserved locations, producing a smooth risk map for the whole country.

Conclusion: We have produced a highly plausible and parsimonious model of historical malaria risk for Botswana from point-referenced data from a 1961/2 prevalence survey of malaria infection in 1-14 year old children. After starting with a list of 50 potential variables we ended with three highly plausible predictors, by applying a systematic and repeatable staged variable selection procedure that included a spatial analysis, which has application for other environmentally determined infectious diseases. All this was accomplished using general-purpose statistical software.

Figure 1

Malaria prevalence data. Malaria prevalence of infection in 1 to 14 year old children, in Botswana, during the 1961/62 national survey.

Figure 2

Month of survey during the 1961/62 national malaria survey.

Figure 3

Flow diagram of staged variable selection procedure.

Figure 4

Plots of malaria prevalence against fourteen potential explanatory variables. Scatter – and box plots of candidate environmental explanatory variables used in step-wise procedures. Malaria prevalence in 1 to 14 year old children, Botswana, 1961/62, is shown on the Y axis on a logit scale. (A) annual maximum rainfall (mm); (B) winter (April – October) total rainfall (mm); (C) rainfall concentration (%); (D) winter (April – October) mean temperature (°C); (E) annual maximum temperature (°C); (F) temperature proportional standard deviation (°C); (G) elevation (m); (H) annual maximum NDVI; (I) NDVI standard deviation; (J) summer (December–March) mean vapour pressure (hPa); (K) vapour pressure standard deviation (hPa); (L) log distance to permanent water (m); (M) land cover: dry/low risk, moist/high risk areas; (N) start month of survey.

Figure 5

Distribution of coefficients of fourteen candidate variables in 1000 stepwise bootstrap models. Frequency histograms of coefficients obtained in automated backward stepwise exclusion regression analysis against 1000 bootstrap samples of the malaria prevalence data in Stage 3. In each case the vertical black line indicates coefficient = 0. (A) annual maximum rainfall (mm); (B) winter (April – October) total rainfall (mm); (C) rainfall concentration (%); (D) winter (April – October) mean temperature (°C); (E) annual maximum temperature (°C); (F) temperature proportional standard deviation (°C); (G) elevation (m); (H) annual maximum NDVI; (I) NDVI standard deviation; (J) summer (December–March) mean vapour pressure (hPa); (K) vapour pressure standard deviation (hPa); (L) log distance to permanent water (m); (M) land cover: dry/low risk, moist/high risk areas; (N) start month of survey: main season (April–May).

Figure 6

Predicted versus observed prevalence. Predicted versus observed prevalence, on a logit scale, for the derivation (crosses) and validation (squares) data of the Stage 5 non-spatial model, and for the median (closed circles) and upper/lower confidence interval (spikes) of the Stage 6 spatial model.

Figure 7

Maps of predicted malaria prevalence and covariates. Predicted pre-control childhood malaria prevalence maps for Botswana, resulting from (A) the stage 5 non-spatial model and (B) the stage 6 spatial model; 118 survey sites are shown; (C) the upper and lower 95% CI of the spatial model. Co-variates used in the models: (D) annual mean temperature, C; (E) summer total rainfall, mm; (F) elevation, m; (G) land cover categories, high-risk/low-risk. Lines represent district boundaries.