Second cancers after fractionated radiotherapy: stochastic population dynamics effects

Abstract

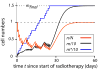
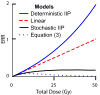
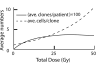
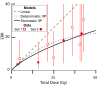
When ionizing radiation is used in cancer therapy it can induce second cancers in nearby organs. Mainly due to longer patient survival times, these second cancers have become of increasing concern. Estimating the risk of solid second cancers involves modeling: because of long latency times, available data is usually for older, obsolescent treatment regimens. Moreover, modeling second cancers gives unique insights into human carcinogenesis, since the therapy involves administering well-characterized doses of a well-studied carcinogen, followed by long-term monitoring. In addition to putative radiation initiation that produces pre-malignant cells, inactivation (i.e. cell killing), and subsequent cell repopulation by proliferation, can be important at the doses relevant to second cancer situations. A recent initiation/inactivation/proliferation (IIP) model characterized quantitatively the observed occurrence of second breast and lung cancers, using a deterministic cell population dynamics approach. To analyze if radiation-initiated pre-malignant clones become extinct before full repopulation can occur, we here give a stochastic version of this IIP model. Combining Monte-Carlo simulations with standard solutions for time-inhomogeneous birth-death equations, we show that repeated cycles of inactivation and repopulation, as occur during fractionated radiation therapy, can lead to distributions of pre-malignant cells per patient with variance>>mean, even when pre-malignant clones are Poisson-distributed. Thus fewer patients would be affected, but with a higher probability, than a deterministic model, tracking average pre-malignant cell numbers, would predict. Our results are applied to data on breast cancers after radiotherapy for Hodgkin disease. The stochastic IIP analysis, unlike the deterministic one, indicates: (a) initiated, pre-malignant cells can have a growth advantage during repopulation, not just during the longer tumor latency period that follows; (b) weekend treatment gaps during radiotherapy, apart from decreasing the probability of eradicating the primary cancer, substantially increase the risk of later second cancers.

FIG. 1. Influences on carcinogenesis risks: initiation, inactivation, and proliferation

Radiation carcinogenesis involves radiation initiation that makes normal cells pre-malignant (Panel A). In radiotherapy, because of the high doses used, a significant fraction of the pre-malignant cells initiated by previous fractions in nearby tissue, and of the normal cells at risk for initiation in subsequent dose-fractions, are inactivated by radiation (Panel B). After cell inactivation, repopulation via symmetric proliferation occurs (Panel C). Repopulation tends to increase second cancer risks for two reasons: a) among the proliferating cells are some pre-malignant ones; and b), proliferation replenishes the pool of normal cells at risk for initiation in subsequent fractions. The classic initiation/inactivation model for second tumors, given by Eqs. (1) and (3), does not take proliferation into account; it predicts very low carcinogenesis risk at sufficiently high doses, due to inactivation. However, initiation/inactivation/proliferation (IIP) models for second tumors take repopulation into account and predict substantial carcinogenesis risks at high doses, due to proliferation counteracting inactivation.

FIG. 2. Deterministic cell repopulation dynamics and the compensation theorem

Normal, and radiation-initiated pre-malignant, average stem cell numbers, n(t) and m(t) respectively, rescaled for convenience, are shown as a function of time since the start of radiotherapy. Calculations were done using the deterministic IIP model (Appendix B) with the following parameters: fraction number K =20 acute dose-fractions, starting on a Monday and continuing daily except for Saturdays and Sundays; dose per fraction to a nearby organ d=1 Gy; initiation constants a=0.75 Gy^-1, b=0; relative fitness of pre-malignant cells r=1; inactivation constants α= 0.3 Gy^-1 and β = 0.025 Gy^-2; and repopulation maximum-rate constant λ=0.3 day^-1. In this deterministic IIP model the numerical value of a is not needed for estimates of ERR (due to renormalizing by referring to atom bomb survivor data, as discussed in the text), but the value of a does matter to the numerical value of m, and we here chose an illustrative value of a. A numerical estimate of the setpoint number N is not needed because the only way n(t) and N appear in the calculations is via the ratio ν = n/N (Appendix B); presumably N≈10⁷ or more in most cases. It is seen that according to the model some normal stem cells (n, red curve) are inactivated in each dose-fraction; then symmetric proliferation causes some repopulation between fractions, especially on weekends. After radiotherapy stops, n grows back to the setpoint number N. Predictions for the average pre-malignant cell number (m, black curve) are the following: at first m grows due to initiation and symmetric proliferation; as m grows, inactivation increases proportionately and starts to overpower initiation; at that point the only effect that tends to increase m is symmetric proliferation, especially during a weekend; finally, after treatment stops, m resumes growth. It is seen that by t = 60 days, repopulation has essentially run its full course. In the text we refer to this time as the “final” time and identify m(60 days) with m_final. In the formal calculations, the difference between m(60) and m(∞) is negligible. However, in this context “final” refers to the comparatively short, radiotherapy time scale only. For the long (multiyear) time scale latency period during which a pre-malignant clone progresses into a clinical cancer, 60 days would actually count as the initial time instead. We do not model such progression mechanistically here, circumventing such modeling by the use of the factor B in Eq. (1), and will thus use the word “final” as specified above. The blue curve, for pre-malignant cell number m*, shows a hypothetical situation in which only initiation occurs at each dose fraction, with α=0=β that no inactivation occurs (and thus there is so also no subsequent repopulation). Then m* simply grows in 20 equal steps. It is seen that ultimately m and m* reach exactly the same value m_final = Kad, illustrating in this special case the result that, whenever r=1, repopulation exactly compensates for inactivation (Appendix A, Theorem 1). For r≠1, however, the interplay between initiation, inactivation, and proliferation means computer algorithms are needed to evaluate m_final even in the deterministic IIP model.

FIG. 3. Different models of ERR

Four models of ERR are shown. We show the case where all four agree at low doses, i.e. the slope of all four curves are the same at the origin, because all four models use renormalization (based on atomic bomb survivor data) at low doses. When extrapolated to higher doses, the models give different results. The parameters used are: K=25 acute dose-fractions, starting on a Monday and continuing daily except for Saturdays and Sundays; initiation factors a= 0.004 per Gy, b=0; relative fitness r=1.2; inactivation constants α= 0.1 Gy^-1 and β= 0; rate constant λ=0.3 day^-1; and ratio of death rate to birth rate c=0.2. Only the stochastic initiation/inactivation/proliferation (IIP) model requires all of these parameters; for example Eq. (3) contains only a, b,α, and β. To show qualitative trends, the figure here compares different models holding common parameters fixed. If any one of the models is used in fitting data, some parameters are adjusted to fit the situation, and the adjustments would usually lead to different parameters for different models fitting the same data (see Fig. 5 for an example). Reading from top to bottom, the deterministic IIP model (blue curve), using mean pre-malignant cell number, shows an increase in ERR at high doses. This is attributed to a growth advantage that the pre-malignant cells have (r>1), which comes into play especially at high doses. The linear model (dashed red line) just extrapolates the low dose slope to high doses. According to the compensation theorem proved in Appendix A, a deterministic IIP model with r=1 (instead of r=1.2) and any values for its other parameters would give this linear curve. The stochastic IIP model (black solid curve), based on presence or absence of pre-malignant cells, has slope decreasing as dose increases, despite the growth advantage. Finally, the older model (dotted blue curve), given by Eq. (3), predicts almost no ERR at high doses, putatively due to inactivation of pre-malignant cells wholly uncompensated by proliferation (Fig. 1).

FIG. 4. Predicted properties of clones

The figure shows predictions of the stochastic IIP model with the same parameters as those used for Fig. 3. The average number of radiation-initiated pre-malignant clones per patient is shown (rescaled for convenience in graphing, the actual maximum is ~0.04 pre-malignant clones per patient). It is seen that at high doses the predicted number of pre-malignant clones per patient does not increase, clones made in earlier dose-fractions being eradicated by later dose-fractions. However, the average number of radiation-initiated, pre-malignant cells per patient continues to increase, as the average number of cells in those clones that do happen to survive increases due to repopulation (i.e. to proliferation following inactivation).

FIG. 5. Comparing different models with data on second breast cancers

The data sets used, set 1 (Travis et al., 2003) and set 2 (van Leeuwen et al., 2003), are described in the Methods section. The figure shows predictions, all of which use K=25 acute dose-fractions, starting on a Monday and continuing daily except for Saturdays and Sundays. For the deterministic IIP model (dotted blue curve), the relative fitness for initiated, and thus pre-malignant, cells is r=0.825; the initiation constants are a= 0.004 Gy^-1 and b=0; the linear inactivation constant is α= 0.18 Gy^-1; the quadratic inactivation constant is β=0; and the proliferation rate constant is λ=0.4 day^-1. By the theorem in Appendix A, the linear model (dashed brown curve) would result from r=1 in the deterministic IIP model with the given initial slope. For the stochastic IIP model (solid black curve) values used are r=2 (i.e. pre-malignant cells have a strong growth advantage), initiation constants a= 0.004 Gy^-1 and b=0 as before, α= 0.075 Gy^-1 and β=0 (i.e. low radiation sensitivity), λ=1.5 day^-1 (i.e. rapid repopulation), and a ratio c=0.2 of death rate parameter to birth rate parameter for pre-malignant cells. For all three curves, the slope at the origin is determined using data on atomic bomb survivors (see text)