Inferring cellular networks--a review
- PMID: 17903286
- PMCID: PMC1995541
- DOI: 10.1186/1471-2105-8-S6-S5
Inferring cellular networks--a review
Abstract
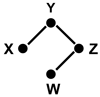
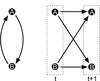
In this review we give an overview of computational and statistical methods to reconstruct cellular networks. Although this area of research is vast and fast developing, we show that most currently used methods can be organized by a few key concepts. The first part of the review deals with conditional independence models including Gaussian graphical models and Bayesian networks. The second part discusses probabilistic and graph-based methods for data from experimental interventions and perturbations.
Figures
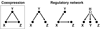
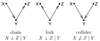


Similar articles
-
Bayesian dynamic multivariate models for inferring gene interaction networks.Conf Proc IEEE Eng Med Biol Soc. 2006;2006:2041-4. doi: 10.1109/IEMBS.2006.260091. Conf Proc IEEE Eng Med Biol Soc. 2006. PMID: 17946930
-
Inferring gene regulatory networks with time delays using a genetic algorithm.Syst Biol (Stevenage). 2005 Jun;152(2):67-74. doi: 10.1049/ip-syb:20050006. Syst Biol (Stevenage). 2005. PMID: 17044234
-
GenePro: a Cytoscape plug-in for advanced visualization and analysis of interaction networks.Bioinformatics. 2006 Sep 1;22(17):2178-9. doi: 10.1093/bioinformatics/btl356. Bioinformatics. 2006. PMID: 16921162
-
Graphs in molecular biology.BMC Bioinformatics. 2007 Sep 27;8 Suppl 6(Suppl 6):S8. doi: 10.1186/1471-2105-8-S6-S8. BMC Bioinformatics. 2007. PMID: 17903289 Free PMC article. Review.
-
Prediction of protein-protein interaction networks.Curr Protoc Bioinformatics. 2003 May;Chapter 8:Unit8.2. doi: 10.1002/0471250953.bi0802s01. Curr Protoc Bioinformatics. 2003. PMID: 18428709 Review.
Cited by
-
Unique ability of pandemic influenza to downregulate the genes involved in neuronal disorders.Mol Biol Rep. 2015 Sep;42(9):1377-90. doi: 10.1007/s11033-015-3916-4. Epub 2015 Aug 6. Mol Biol Rep. 2015. PMID: 26246405
-
DRAGON: Determining Regulatory Associations using Graphical models on multi-Omic Networks.Nucleic Acids Res. 2023 Feb 22;51(3):e15. doi: 10.1093/nar/gkac1157. Nucleic Acids Res. 2023. PMID: 36533448 Free PMC article.
-
Reverse engineering and identification in systems biology: strategies, perspectives and challenges.J R Soc Interface. 2013 Dec 4;11(91):20130505. doi: 10.1098/rsif.2013.0505. Print 2014 Feb 6. J R Soc Interface. 2013. PMID: 24307566 Free PMC article. Review.
-
A parallel algorithm for reverse engineering of biological networks.Integr Biol (Camb). 2011 Dec;3(12):1215-23. doi: 10.1039/c1ib00117e. Epub 2011 Nov 14. Integr Biol (Camb). 2011. PMID: 22080176 Free PMC article.
-
Modeling of Interactions between Cancer Stem Cells and their Microenvironment: Predicting Clinical Response.Methods Mol Biol. 2018;1711:333-349. doi: 10.1007/978-1-4939-7493-1_16. Methods Mol Biol. 2018. PMID: 29344897 Free PMC article. Review.
References
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

