Dimensional reduction in sensorimotor systems: a framework for understanding muscle coordination of posture

Abstract

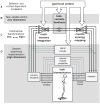
The simple act of standing up is an important and essential motor behavior that most humans and animals achieve with ease. Yet, maintaining standing balance involves complex sensorimotor transformations that must continually integrate a large array of sensory inputs and coordinate multiple motor outputs to muscles throughout the body. Multiple, redundant local sensory signals are integrated to form an estimate of a few global, task-level variables important to postural control, such as body center of mass (CoM) position and body orientation with respect to Earth-vertical. Evidence suggests that a limited set of muscle synergies, reflecting preferential sets of muscle activation patterns, are used to move task-variables such as CoM position in a predictable direction following postural perturbations. We propose a hierarchical feedback control system that allows the nervous system the simplicity of performing goal-directed computations in task-variable space, while maintaining the robustness afforded by redundant sensory and motor systems. We predict that modulation of postural actions occurs in task-variable space, and in the associated transformations between the low-dimensional task-space and high-dimensional sensor and muscle spaces. Development of neuromechanical models that reflect these neural transformations between low- and high-dimensional representations will reveal the organizational principles and constraints underlying sensorimotor transformations for balance control, and perhaps motor tasks in general. This framework and accompanying computational models could be used to formulate specific hypotheses about how specific sensory inputs and motor outputs are generated and altered following neural injury, sensory loss, or rehabilitation.

Figure 1. Muscle activity evoked following perturbations to the support-surface

A) Backward perturbations of the support surface elicit activity in muscles on the posterior side of the body. Forward perturbations elicit activity in muscles on the anterior side of the body. The gray area represents the initial muscular response to perturbation, called the automatic postural response (APR). Note that at the onset of the APR, the amplitude of platform and center of mass displacement are quite small. B) The magnitude of the response during the APR varies as a function of direction and can be plotted as a tuning curve. Each muscle has a unique tuning curve, suggesting that each muscle is activated by a separate neural command signal.

Figure 2. Illustration demonstrating that local muscle stretch cannot predict postural responses

A) In translation perturbations of the support surface, the muscle stretch and postural response occur in the same muscles—in the case of backward perturbations, the triceps surae. B) In rotation perturbations of the support surface, the muscle stretch and the postural response occur in the opposite muscles. In the case of a toes-up rotation, the triceps surae is stretched, but the postural response occurs in the antagonist, the tibialis anterior. Therefore, the short-latency stretch response is possibly destabilizing. C) In toes-down perturbations of the support surface, the postural response occurs in the triceps surae muscle, the same as in the backward translation in A. In both cases, the center of mass is displaced in the forward direction relative to the base of support, requiring triceps surae activation. The direction of this more global, task-level variable that is not directly detected by any one sensory modality is the best predictor of muscle activation patterns during postural responses. (Illustration after Nashner 1976)

Figure 3. Comparison of “fixed” versus “flexible” muscle synergy concepts

A) In the original muscle synergy concept, only one muscle synergy was elicited at a time, and muscles could only be activated by one synergy. Therefore, all muscles activated by the same synergy would have the same tuning curve, determined by the neural command, C_i, that activated it. B) In the new concept, more than one synergy can be activated at a time. Further, muscles can participate in multiple synergies, and have different weightings in each synergy. Each muscle’s tuning curve is a weighted average of the two tuning curves of each muscle synergy. This allows flexibility in muscle tuning curves while also reducing the dimension of the neural control task.

Figure 4. Two postural strategies for controlling the center of mass in response to backward perturbations of the support surface

The two postural strategies are characterized by different joint motions and muscle activation patterns. A) In the ankle strategy, motion is restricted to the ankle joint, and muscles on the posterior side of the body are activated. B) In the hip strategy, the hip is flexed and muscles on the anterior side of the body are activated, but at longer latencies than in the ankle strategy. These two strategies represent extremes of a continuum, and a mixture of the two strategies can be observed in most postural responses (Creath et al., 2005, Runge et al., 1999).

Figure 5. Muscle synergies robustly produce endpoint forces in cat postural control

A) Five muscle synergy vectors, W_i, extracted from postural responses to support surface translation at the preferred stance distance in cat Bi. These five muscle synergies account for over 96% of the total variability accounted for in the preferred stance. Each bar represents the relative level of activation for each muscle within the synergy. Note that muscles can contribute to multiple muscle synergies. B) Activation coefficients, C_i, representing the purported neural commands to each muscle synergy during postural responses in four different postural configuration. Upper traces show background activity of each muscle synergy during the quiet stance period before perturbations. Lower traces show the synergy tuning curves in response to support surface translations. Changes in muscle tuning curves at different stance distances are due to variations in the amplitude of the neural commands to the various muscle synergies. Some muscle synergies (e.g. red, yellow) are relatively constant amplitude across all conditions, whereas others (e.g. green, purple) are highly modulated. C) Endpoint force vectors produced by each muscle synergy (same color coding), in the sagittal, frontal, and horizontal planes. Vectors are expressed as forces applied by the limb against the support surface. The amplitude of each the force vectors in any postural response is directly modulated by the amplitude of the neural command to each muscle synergy. (Adapted from Torres-Oviedo et al. 2006.)

Figure 6. Muscle tuning curves reconstructed using the same set of muscle synergies in four different postural configurations

Muscle tuning curves vary across postural responses to support surface perturbation when postural configuration is varied. These variations can be reconstructed using the set of muscle synergies extracted from the preferred stance configuration. The original data are shown by the dashed black line, and the reconstructed data by the solid black line. The contribution from each synergy to the reconstruction is shown by the corresponding colored line. This is computed by multiplying each functional synergy vector W by its activation coefficient C. (Adapted from Torres-Oviedo et al. 2006.)

Figure 7. Example of similar dimensional-reduction and task-variable encoding across individuals

In all cats, 5 synergies accounted for >96% of the variability in response to translation at the preferred stance. A) Muscle synergies for each individual. Colored bars indicate muscles that were measured across all individuals. Gray bars indicate the remaining muscles collected for each individual. While there are general similarities in the most highly activated muscles in each synergy, substantial variation in muscles contributing to the synergies exist across individuals. B) Activation coefficients across animals are similar, indicating that they are activated in similar perturbation directions. C) Force vectors produced by each synergy are also quite similar. Taken together, this data demonstrates that neural commands encoding force-vector directions are quite similar across individuals, but the specific muscle synergy mapping used can vary. (Adapted from Torres-Oviedo et al. 2006.)

Figure 8

General framework for understanding dimensional reduction in muscle coordination of posture. The framework consists of a nested set of hierarchal feedback loops with much lower dimensionality at the higher levels than the lower levels. A) Goal-level modulation of postural responses occurs in task-variable space. Therefore behavioral or cognitive-level modulation can alter the task-variables attended to, as well as the way they are estimated and regulated by B) low dimensional feedback in the case of postural control. C) Mappings between low- and high-dimensional spaces are necessary for estimation and control of task-level variables. A dimensional reduction occurs in the multisensory integration mappings that use multiple afferent signals to estimate task-variables. Once the desired effect on the task-level variable is determined, a dimensional expansion occurs via muscle synergy mappings, allowing the action to be implemented in D) specific anatomical details. At this level there are many nonlinearities and state-dependent effects that can influence the eventual biomechanical output produced through the activation of a muscle synergy. However, some of these factors, such as spinal circuits, may be used to make the system more controllable by the reduced-dimension controller, and are also influenced by higher-level centers. This general framework can be used to make specific hypotheses about the characteristics of changes in muscle activation patterns in postural responses due to changes at all levels in the nervous system. In addition, it can be used to guide computational studies focused on understanding mappings to and from the low-dimensional space where movement is controlled by the nervous system.