Modular control of limb movements during human locomotion

Abstract

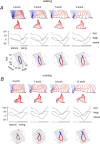
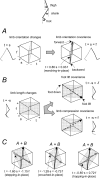
The idea that the CNS may control complex interactions by modular decomposition has received considerable attention. We explored this idea for human locomotion by examining limb kinematics. The coordination of limb segments during human locomotion has been shown to follow a planar law for walking at different speeds, directions, and levels of body unloading. We compared the coordination for different gaits. Eight subjects were asked to walk and run on a treadmill at different speeds or to walk, run, and hop over ground at a preferred speed. To explore various constraints on limb movements, we also recorded stepping over an obstacle, walking with the knees flexed, and air-stepping with body weight support. We found little difference among covariance planes that depended on speed, but there were differences that depended on gait. In each case, we could fit the planar trajectories with a weighted sum of the limb length and orientation trajectories. This suggested that limb length and orientation might provide independent predictors of limb coordination. We tested this further by having the subjects step, run, and hop in place, thereby varying only limb length and maintaining limb orientation fixed, and also by marching with knees locked to maintain limb length constant while varying orientation. The results were consistent with a modular control of limb kinematics where limb movements result from a superposition of separate length- and orientation-related angular covariance. The hypothesis finds support in the animal findings that limb proprioception may also be encoded in terms of these global limb parameters.

Figure 1.

Kinematic patterns during walking (A) and running (B) on a treadmill at different speeds. Top to bottom, Stick diagrams for a single stride (blue during stance and red during swing; swing phase referenced to hip joint); ensemble averages (±SD; n = 8 subjects) of thigh, shank, and foot elevation angles of the right leg and corresponding trajectories in segment angle space (swing phase is red) along with the interpolated plane. Paths progress in time in the counterclockwise direction, touch down and lift-off corresponding approximately to the top and bottom of the loop, respectively.

Figure 2.

Kinematic patterns during over-ground locomotor movements. A, Kinematic patterns of different gaits at a natural cadence in one representative subject. Top to bottom, Stick diagrams, thigh, shank, and foot elevation angles of the right leg, and corresponding trajectories in segment angle space along with the interpolated plane. For air-stepping, we simulated the speed of progression equivalent to the horizontal speed of foot motion during midstance, 3.1 km/h for this subject. The interpolation plane results from orthogonal planar regression: the first eigenvector (u ₁) is aligned with the long axis of the gait loop, the second eigenvector (u ₂) is aligned with the short axis, and the third eigenvector (u ₃) is the normal to the plane. B, Spatial distribution of the normal to the plane for each gait. Each circle on the sphere surface corresponds to the projection of the mean plane normal (the center of the circle) onto the unit sphere the axes of which are the direction cosines with the semiaxis of the thigh, shank, and foot. The radius of the circles correspond to the angular SD across subjects (n = 8). The angles of cones correspond to 2 SDs, accordingly. The foot semiaxis is positive, and the thigh and shank semiaxes are negative.

Figure 3.

PCA of elevation angles during over-ground locomotor movements. A, Covariance planes from Figure 2 with the directions of the PCs superimposed (black arrows). Directions of rotated PCs (PC*) (see Appendix and C) are shown in color (PC₁* in blue; PC₂* in red). B, Two principal components (PC₁ and PC₂; solid lines) and their correlations with limb length (GT-VE) and limb angle (dotted lines). C, Rotated PCs and their correlations with limb length and limb angle. PC₁* was approximated by projecting the data to the hypothetical limb orientation covariance line (t = s = f), and PC₂* was obtained by projecting the data to the in-place experimental covariance line (red). For air-stepping, subjects executed small horizontal foot excursions (∼15–20 cm) when stepping in-place in the air; accordingly, there was an ellipse rather than a line. In this case, we took the orientation of the long axis of the ellipse as an approximation of the direction of the limb length covariance.

Figure 4.

Kinematic patterns of in-place movements at a natural cadence and knee-locked marching by one representative subject. A, Kinematic patterns. During stepping, hopping, crouched in place, and knee-locked marching, the trajectory loop reduces to a line (see Results). During running, there is a small deviation from the line in stance, and during air-stepping, the trajectory is a loop, because subjects could not suppress some horizontal movement. B, Two principal components (PC₁ and PC₂; solid lines) and their correlations with limb length (GT-VE) and limb angle (dotted lines). During in-place movements, the limb angle was nearly constant, and the limb length varied as shown by the dotted line. During marching, the limb orientation varied, and the limb length was nearly constant. The first principal component of the linear trajectory is highly correlated with changes in the limb length for each in-place gait. The first principal component is correlated with the limb orientation for marching.

Figure 5.

Linear combination of segment angle covariance during in-place movements with limb orientation obtained during actual locomotor movements. Left column, Over-ground kinematic patterns during walking, running, and hopping in one representative subject. Middle column, Limb (GT-VE) orientation waveforms correspond to walking at 5 km/h, running at 9 km/h, and hopping at 4 km/h. Right column, Comparison of actual kinematic patterns during in-place stepping, running, and hopping with those predicted by subtracting the respective limb orientation from the over-ground trajectories. Waveform correlation coefficients (r) for each pair listed at the far right.

Figure 6.

A simple model of additive limb segment angle covariances. A, Limb orientation basic covariance with t = s = f (black line) compared with the average linear trajectory for marching (t = 0.86 · s = 0.93 · f; brown). B, Limb length basic covariance (along the line t = −s) leading to a foot lift covariance with shank and foot segments in phase (t = −s = −f; dashed black line) and a limb compression covariance with shank and foot out of phase (t = −s = f; dashed black line). C, Examples of additive covariance. Linear combinations of elementary covariance vectors result in planar covariance patterns (gray planes) resembling those observed during walking, hopping, and crouched walking (compare with Fig. 2 A). The in-place linear trajectories averaged across subjects were: t = −1.60 · s = −1.15 · f for stepping in place (blue), t = −1.28 · s = −0.72  · f for crouched stepping in place (gray), and t = −0.85 · s = 0.72 · f for hopping in place (green). Elevation angles: t, thigh; s, shank; f, foot.

Figure 7.

General foot placement characteristics and association of plane trajectories of the segment angles with endpoint motion. A, Left panel, Foot orientation (gray triangles formed by connecting LM-VM-HE markers) and ground reaction forces (upward pointing vectors) during over-ground walking, running, and hopping at a natural speed plotted every 14% of the gait cycle in one representative subject. Middle panel, Averaged (±SD; n = 8 subjects) time course of the instantaneous position of the COP relative to the foot during stance. Right panel, Excursion and mean position (asterisk) of the COP for each gait. B, Stick diagram, gait loop (for walking), and virtual endpoint trajectories obtained from PC₁* and PC₂* (see Appendix). Mapping of the polar coordinates of the limb axis (left) to the coordinates of the covariance plane (right) is shown for walking using the grid. Limb orientation (t = s = f) and limb length (stepping in-place) covariance directions are indicated. Note an oblique orientation of the two axes. In the bottom panel, virtual endpoint trajectories obtained from PC₁* and PC₂* and transformed to the foot frame are shown for walking, running, and hopping in one representative subject. Asterisks denote mean COP positions during stance in each gait.