Analytical and numerical quantification and comparison of the local electric field in the tissue for different electrode configurations

Abstract

Background: Electrochemotherapy and gene electrotransfer are novel promising treatments employing locally applied high electric pulses to introduce chemotherapeutic drugs into tumor cells or genes into target cells based on the cell membrane electroporation. The main focus of this paper was to calculate analytically and numerically local electric field distribution inside the treated tissue in two dimensional (2D) models for different plate and needle electrode configurations and to compare the local electric field distribution to parameter U/d, which is widely used in electrochemotherapy and gene electrotransfer studies. We demonstrate the importance of evaluating the local electric field distribution in electrochemotherapy and gene electrotransfer.

Methods: We analytically and numerically analyze electric field distribution based on 2D models for electrodes and electrode configurations which are most widely used in electrochemotherapy and gene electrotransfer. Analytical calculations were performed by solving the Laplace equation and numerical calculations by means of finite element method in two dimensions.

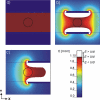
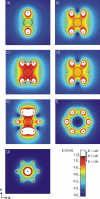
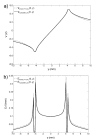
Results: We determine the minimal and maximal E inside the target tissue as well as the maximal E over the entire treated tissue for the given electrode configurations. By comparing the local electric field distribution calculated for different electrode configurations to the ratio U/d, we show that the parameter U/d can differ significantly from the actual calculated values of the local electric field inside the treated tissue. By calculating the needed voltage to obtain E > U/d inside the target tissue, we showed that better electric field distribution can be obtained by increasing the number and changing the arrangement of the electrodes.

Conclusion: Based on our analytical and numerical models of the local electric field distribution we show that the applied voltage, configuration of the electrodes and electrode position need to be chosen specifically for each individual case, and that numerical modeling can be used to optimize the appropriate electrode configuration and adequate voltage. Using numerical models we further calculate the needed voltage for a specific electrode configuration to achieve adequate E inside the target tissue while minimizing damages of the surrounding tissue. We present also analytical solutions, which provide a convenient, rapid, but approximate method for a pre-analysis of electric field distribution in treated tissue.

Figure 1

Three geometries with parallel plate electrodes analyzed in this study (d = 8.66 mm).

Figure 2

Different needle electrode configurations analyzed in this study.

Figure 3

Calculated electric field distribution for the geometries with parallel plate electrodes. Numerical results of the electric field distribution for geometries defined in Fig. 1: a) the infinite plate electrodes case, b) the target tissue symmetrically placed between the finite plate electrodes and c) the non-symmetrical example when the target tissue is not entirely in-between the finite plate electrodes. The circle represents the target tissue e.g. tumor tissue and the white region represents part of tissue where E ≥ U/d.

Figure 4

Calculated electric field distribution for different needle electrode configurations. Numerical results of the electric field distribution for the geometries defined in Fig. 2: a) two needle electrodes, b) four needle electrodes, c) six needle electrodes in two rows, d) six electrodes placed in a circle with polarities as shown in Fig. 2d, e) six needle electrodes placed in a circle with polarities as shown in Fig. 2e, f) seven needle electrodes placed in a circle – using alternating polarities seven needle electrodes placed in a circle – with central positive and surrounding electrodes having negative polarities and g) seven needle electrodes placed in a circle – with central positive and surrounding electrodes having negative polarities. In all cases the applied voltage was set in such a way that U/d = 1.15 V/cm, where d = 8.66 mm for Figs. 4a, 4b, 4c, 4d and 4e and d = 5 mm for Figs. 4f and 4g. The circle represents the target tissue and the white region represents part of tissue where E ≥ U/d.

Figure 5

Comparison of the analytical and the numerical solution. The analytical and the numerical solutions of a) the electric potential and b) electric field distribution along y axis (x = 0) for applied voltage U = 1 V (V₊ = 0.5 V, V_- = - 0.5 V) are given for the configuration defined in Fig. 2c.

Figure 6

Calculated electric field distribution for in-homogeneous models. Numerical results of the electric field distribution for needle electrode configurations defined in Figs. 2a-2c: a) two needle electrodes, b) four needle electrodes, c) six needle electrodes in two rows taking into account two-times higher conductivity of the target tissue compared to surrounding tissue (conductivity of the target tissue is σtt = 0.4 S/m and conductivity of the surrounding tissue σst = 0.2 S/m). In all cases the applied voltage was set in such a way that U/d = 1.15 V/cm.