Experimental test of scaling of mixing by chaotic advection in droplets moving through microfluidic channels

Abstract

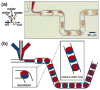
This letter describes an experimental test of a simple argument that predicts the scaling of chaotic mixing in a droplet moving through a winding microfluidic channel. Previously, scaling arguments for chaotic mixing have been described for a flow that reduces striation length by stretching, folding, and reorienting the fluid in a manner similar to that of the baker's transformation. The experimentally observed flow patterns within droplets (or plugs) resembled the baker's transformation. Therefore, the ideas described in the literature could be applied to mixing in droplets to obtain the scaling argument for the dependence of the mixing time, t~(aw/U)log(Pe), where w [m] is the cross-sectional dimension of the microchannel, a is the dimensionless length of the plug measured relative to w, U [m s(-1)] is the flow velocity, Pe is the Péclet number (Pe=wU/D), and D [m(2)s(-1)] is the diffusion coefficient of the reagent being mixed. Experiments were performed to confirm the scaling argument by varying the parameters w, U, and D. Under favorable conditions, submillisecond mixing has been demonstrated in this system.

FIG. 1

(Color) Mixing by the baker’s transformation in plugs moving through winding microfluidic channels shown (a) experimentally and (b) schematically. (a) Left: a scheme of the microfluidic network. Right: microphotograph of plugs. Solutions were as in Fig. 3 of Ref. . Total flow velocity U=53 mm s⁻¹.

FIG. 2

(Color) An illustration of mixing in plugs moving through microchannels and quantification of the mixing. (a) and (b) Left: a scheme of the microfluidic network. (a) Right: microphotograph showing flow patterns in plugs moving through the microchannels used to test the scaling argument. (b) Right: a false-color fluorescence microphotograph of plugs showing time-averaged fluorescence arising from mixing of Fluo-4 and Ca²⁺ solutions (see Ref. 1). (c) Mixing curve obtained by analyzing intensities of fluorescence in images such as shown in (b). Submillisecond mixing was observed for the specified conditions of w, U, and D.

FIG. 3

(Color) Experimental data testing the scaling of chaotic mixing. (a)–(d) 90% mixing time (90% t_mix [s]), was obtained from mixing curves such as shown in Fig. 2(c). Mixing time as a function of (a) w (symbols) for constant U=100 mm s⁻¹; (b) U for constant w=100 μm; and (c) D for constant w=100 μm and varying U from 18 mm s⁻¹ (open symbols) to 66 mm s⁻¹ (closed symbols). Data are shown for □ D∼1.6×10⁻⁹ m² s⁻¹ obtained with the Fluo-4/Ca²⁺ system, and for ⋄ D∼2×10⁻¹⁰ m² s⁻¹ obtained with the RNase A system. (d) Entire data set from (a)–(c) is replotted versus (w/2)²/2D, where stl(0)∼w/2. This plot demonstrates that the observed mixing by chaotic advection is much faster than would have been predicted if mixing occurred purely by diffusion (prediction of mixing by pure diffusion is shown by dashed line with a slope of 1).

FIG. 4

(Color) Entire experimental data set from Fig. 3 collapses on a line when plotted versus (w/U)log(Pe), in agreement with the scaling equation.