Identification and classification of hubs in brain networks

Abstract

Brain regions in the mammalian cerebral cortex are linked by a complex network of fiber bundles. These inter-regional networks have previously been analyzed in terms of their node degree, structural motif, path length and clustering coefficient distributions. In this paper we focus on the identification and classification of hub regions, which are thought to play pivotal roles in the coordination of information flow. We identify hubs and characterize their network contributions by examining motif fingerprints and centrality indices for all regions within the cerebral cortices of both the cat and the macaque. Motif fingerprints capture the statistics of local connection patterns, while measures of centrality identify regions that lie on many of the shortest paths between parts of the network. Within both cat and macaque networks, we find that a combination of degree, motif participation, betweenness centrality and closeness centrality allows for reliable identification of hub regions, many of which have previously been functionally classified as polysensory or multimodal. We then classify hubs as either provincial (intra-cluster) hubs or connector (inter-cluster) hubs, and proceed to show that lesioning hubs of each type from the network produces opposite effects on the small-world index. Our study presents an approach to the identification and classification of putative hub regions in brain networks on the basis of multiple network attributes and charts potential links between the structural embedding of such regions and their functional roles.

Figure 1. Connection matrices and matching index matrices for data sets examined in this study.

Plots show structural connections (left panels) and matching index (right panels). Connection patterns are represented as binary connection matrices C_ij, with existing connections (edges) indicated by a filled (black) square (c_ij = 1). No distinction is made between connections that have been shown to be absent and connections that are unknown; all are represented by a white square (c_ij = 0). Main diagonals are indicated in grey and self-connections are excluded (c_ii = 0). From top to bottom: (A) Macaque cortex (N = 47, K = 505). (B) Cat cortex (N = 52, K = 820). Panels on the right show the matching index matrix M_ij calculated from the connection matrix following Hilgetag et al. . The matching index scales between 0 (no match) and 1 (perfect match), and m_ij = m_ji. The arrangement of brain regions for each of the four matrices was arrived at as follows. The M_ij matrix was converted to a distance matrix, from which a hierarchical cluster tree was computed using a consecutive linking procedure based on farthest inter-cluster distances. This resulted in a linear ordering of areas based on cluster membership and inter-cluster distances. The ordering was rotated such that visual areas appear topmost.

Figure 2. Degree of areas in macaque and cat cortex.

The degree of each area of macaque cortex (A) and cat cortex (B) is calculated as the sum over all row and column entries for that area in the matrix of structural connections (Fig. 1). High-degree areas are all areas with a degree greater than the network mean plus one standard deviation. In this, and in all subsequent figures in this paper, these high-degree areas are labeled in yellow.

Figure 3. Statistical significance of motif participation for individual brain regions.

(A) Macaque cortex. (B) Cat cortex. Each plot shows z-scores (half circles, light blue = relative to random networks, dark blue = relative to lattice networks) for each individual area. Areas with significantly positive z-scores for both comparisons are marked in shades of red (see legend). These areas are marked identically in Fig. 4. High-degree areas are marked by yellow arrows. Motif classes of size M = 3 are shown at the upper right of the plot.

Figure 4. Hierarchical cluster analysis of motif fingerprints for individual brain regions.

(A) Dendrogram and clustered motif fingerprints for macaque cortex (top) and cat cortex (bottom). The dendrogram was constructed from the Pearson correlations between all pairs of motif fingerprints (normalized) using a consecutive linking procedure based on farthest inter-cluster distances. This results in a dendrogram with smaller distances for areas with more similar motif fingerprints. Stippled lines mark 2/3-maximal distance, at which cluster boundaries were drawn for subsequent analysis. Motif fingerprints for individual brain regions are arranged vertically by hierarchical cluster distance. Four distinct clusters per network are delineated and clusters with more than 2 members are marked “a”, “b”, “c” for macaque cortex, and “d”, “e”, “f” for cat cortex. (B) The average motif fingerprints for these six clusters are used to perform principal components analysis (PCA); a PCA plot spanning the two largest principal axes is shown. Average motif fingerprints are plotted as segmented circles, with circle size proportional to the number of contributing areas within the cluster, and motif classes represented around the circle (see inset). Note the proximity of several regional clusters with highly similar average motif fingerprints, especially clusters “c” (macaque cortex) and “f” (cat cortex).

Figure 5. Apex ratio for motif and clustering coefficients in macaque and cat cortex.

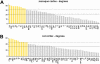
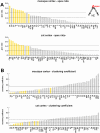
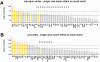
The apex ratio (A) reflects the incidence of a given brain region at the apex (central node) of all motifs of class that the region participates in (see inset). Areas are displayed in decreasing order. High-degree areas are displayed with yellow bars, others are displayed with gray bars. Horizontal lines mark the mean apex ratio (solid line) and the mean plus one standard deviation (dashed line). Panel B shows the ranked clustering coefficient for each area of macaque and cat cortex, with high-degree areas once again shown in yellow. Horizontal lines mark the mean clustering coefficient (solid line) and the mean minus one standard deviation (dashed line).

Figure 6. Centrality measures in macaque and cat cortex.

(A) Betweenness centrality, calculated as the fraction of all shortest paths traveling through a given vertex (see Methods). (B) Closeness centrality, calculated as the inverse of the average length of the shortest paths linking a given vertex to all others in the network (see Methods). Areas are ranked in decreasing order, with high-degree areas shown in yellow. Horizontal lines mark mean centrality (solid line) and mean plus one standard deviation (dashed line).

Figure 7. Hub classification.

(A) Distribution of participation coefficients (see Methods) for each area of macaque and cat cortex, ranked in decreasing magnitude, with high-degree areas shown in yellow. (B,C) Area V4 and area 46 submatrices and projection length distributions. (B, left) Area V4 submatrix, comprised of the subset of areas and connections of the macaque cortex directly connected to area V4. Areas are arranged such that connections are optimally contracted towards the main diagonal, resulting in two clusters containing mostly dorsal (upper left) and mostly ventral (lower right) areas. V4 afferents and efferents are shaded in dark gray. (B, middle) Graph rendering of the V4 submatrix shows that this subnetwork comprises two component clusters with V4 in a central position. Rendering of the graph was performed in Pajek (http://vlado.fmf.uni-lj.si/pub/networks/pajek/; [69]) using the Kamada-Kawai layout algorithm . V4 is marked by a blue dot, members of cluster 1 (mostly dorsal stream visual areas) are marked in white, and members of cluster 2 (mostly ventral stream visual areas) are marked in gray. (B, right) Surface representation of V4 (shaded in blue) and its direct neighbors (shaded in light blue). Histogram shows the distribution of the connection lengths between area V4 and its immediate neighbors. The mean connection length is 17.09 mm (S.D. = 9.60 mm). (C, left) Area 46 submatrix. (C, middle) Pajek plot for area 46 submatrix. Clusters linked by area 46 appear less segregated than those for area V4 and contain a mixture of visual, sensorimotor and multimodal areas. (C, right) Surface representation of area 46 and its neighbors, and histogram of area 46 connection lengths (mean = 33.41 mm, S.D. = 10.58 mm).

Figure 8. Impact of single area lesion on small-world index.

Areas are sorted in decreasing order and high-degree areas are shown in yellow. Horizontal lines mark the mean small-world index of the intact macaque (A) and cat (B) network (solid lines) as well as their respective standard deviations (dashed lines). Error bars show the standard deviations of the distributions of σ_sw after the lesion was made. All distributions for σ_sw were derived from n = 1000 comparisons to degree-matched random networks. Differences at the ends of the spectrum were highly significant (p<10⁻¹⁶); non-significant differences are marked with a cross (×).