Estimating genealogies from linked marker data: a Bayesian approach

Abstract

Background: Answers to several fundamental questions in statistical genetics would ideally require knowledge of the ancestral pedigree and of the gene flow therein. A few examples of such questions are haplotype estimation, relatedness and relationship estimation, gene mapping by combining pedigree and linkage disequilibrium information, and estimation of population structure.

Results: We present a probabilistic method for genealogy reconstruction. Starting with a group of genotyped individuals from some population isolate, we explore the state space of their possible ancestral histories under our Bayesian model by using Markov chain Monte Carlo (MCMC) sampling techniques. The main contribution of our work is the development of sampling algorithms in the resulting vast state space with highly dependent variables. The main drawback is the computational complexity that limits the time horizon within which explicit reconstructions can be carried out in practice.

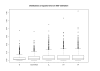
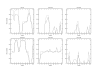
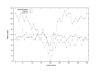
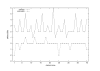
Conclusion: The estimates for IBD (identity-by-descent) and haplotype distributions are tested in several settings using simulated data. The results appear to be promising for a further development of the method.

Figure 1

Pedigree of the first example. 439 individuals and 10 generations of which the youngest one consisted of the children of 13 nuclear families. Squares denote males, circles denote females. Reprinted from [10].

Figure 2

Haplotyping. The development of the sum of switch distances of the haplotype pairs of the youngest generation over 1,000,000 iterations, both with and without using the recombination model. The line at 318 is the expected value under random haplotype assignment and the line at 77 is the value obtained with PHASE (v.2.1).

Figure 3

Squared errors of relatedness estimates. Boxplots show squared errors of all 741 pairwise relatedness coefficients R_ij, where i and j are different individuals from generation 0. The boxes indicate the quartiles (1st, 2nd and 3rd) and the 'whiskers' cover the errors whose distance from the box is less than 1.5 times the box size. The outliers are indicated with single points. Methods used: ours (G), ours without linkage model (G(unlinked)), Lynch and Li's (LL), Lynch and Ritland's (LR) and Wang's (W).

Figure 4

IBD-sharing probabilities R_ij(l) for six pairs of individuals from generation 0. These individuals can be found from Figure 1 where the indexes increase from right to left (from 1 to 39). The two leftmost panels illustrate the IBD-sharing profiles of full-siblings, the upper panel in the middle is of a pair of first cousins, and the lower one describes half cousins. The two rightmost panels show the IBD-sharing between the most distant relatives that can be found in the data. The dotted lines are the exact values and the solid lines our estimates.

Figure 5

IBD-sharing among 44 sampled individuals at each marker locus. The statistic Min($\mathcal{S}$; l) was calculated from the original situation with respect to the 19th generation (original founder level) and the 9th generation and from a reconstruction over 9 generations.

Figure 6

IBS-sharing among 44 sampled individuals at each marker locus. The upper curve illustrates similar statistic as Min($\mathcal{S}$; l) but calculated from IBS-status. The lower curve displays the difference Min($\mathcal{S}$; l) - Min($\mathcal{C}$; l), where $\mathcal{C}$ is a control group. No signal of the trait locus between the markers 20 and 21 can be found from these IBS-statistics.

Figure 7

Haplotype sharing among 44 sampled individuals at each marker locus. HSS is calculated for the original situation with respect to two different founder levels (19th and 9th generations) and for the reconstruction (9 generations). The signal in the reconstruction is very weak compared to the true situation.