Cerebellar motor learning: when is cortical plasticity not enough?

Abstract

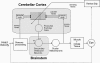
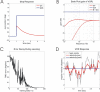
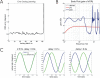
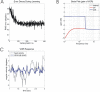
Classical Marr-Albus theories of cerebellar learning employ only cortical sites of plasticity. However, tests of these theories using adaptive calibration of the vestibulo-ocular reflex (VOR) have indicated plasticity in both cerebellar cortex and the brainstem. To resolve this long-standing conflict, we attempted to identify the computational role of the brainstem site, by using an adaptive filter version of the cerebellar microcircuit to model VOR calibration for changes in the oculomotor plant. With only cortical plasticity, introducing a realistic delay in the retinal-slip error signal of 100 ms prevented learning at frequencies higher than 2.5 Hz, although the VOR itself is accurate up to at least 25 Hz. However, the introduction of an additional brainstem site of plasticity, driven by the correlation between cerebellar and vestibular inputs, overcame the 2.5 Hz limitation and allowed learning of accurate high-frequency gains. This "cortex-first" learning mechanism is consistent with a wide variety of evidence concerning the role of the flocculus in VOR calibration, and complements rather than replaces the previously proposed "brainstem-first" mechanism that operates when ocular tracking mechanisms are effective. These results (i) describe a process whereby information originally learnt in one area of the brain (cerebellar cortex) can be transferred and expressed in another (brainstem), and (ii) indicate for the first time why a brainstem site of plasticity is actually required by Marr-Albus type models when high-frequency gains must be learned in the presence of error delay.

Figure 1. Simplified Diagram of the Circuitry That Mediates the Horizontal VOR

Head-velocity signals are processed by the semicircular canals and primary vestibular neurons, relayed to secondary vestibular neurons in the brainstem, and then passed to ocular motoneurons (the classic 3-neuron arc). Motor command signals from the motoneurons control the oculomotor plant, i.e., eye muscles plus orbital tissue, in order to produce eye movements that counteract the effects of the head velocity on the retinal image. Inaccurate eye movements produce retinal slip, which is detected by the visual system. A side loop to the main 3-neuron arc passes through the floccular region of the cerebellum. This region of cerebellar cortex receives as mossy fiber input vestibular information and a copy of the motor command sent to the eye muscles. These mossy fiber inputs are converted into parallel fiber signals by granule cells and associated circuitry in the granular layer, and the parallel fiber signals influence simple spike firing (∼100 spikes/s) in Purkinje cells. Variation in simple spike firing is transmitted to a subset of secondary vestibular neurons (floccular target neurons) in the brainstem. The flocculus also receives a retinal-slip signal as climbing fiber input, which produces low-frequency (∼1 spike/s) complex spikes. Evidence from studies of VOR adaptation suggest that there are two sites of neural plasticity, one in cerebellar cortex and one in brainstem [8,44]. The simplified diagram omits cerebellar interneurons, and shows the efference copy of the motor commands as originating from the oculomotor neurons themselves. In reality this signal appears to originate from a number of areas, in particular the cell groups of the paramedian tracts [–36].

Figure 2. Linearised Model of Horizontal Vestibulo-Ocular Reflex, Derived from the Neural Circuitry Illustrated in Figure 1

(A) Head velocity x(t) is processed by the filter V, then added to the output z(t) of the adaptive filter C (which corresponds to the floccular region of cerebellum). The summed signal is then passed to the brainstem controller B. The output of B is a motor command y(t), which acts on the plant P. A copy of y(t) is sent back to the adaptive filter C. The command y(t) acts on P to move the eyes, a movement which is added to the head velocity x(t): net image movement is detected as retinal slip e(t) and sent to C. (B) Structure of the adaptive filter shown as C in (A). The copy of the eye-movement command y(t) arrives as mossy fiber input, and is decomposed into components y₁(t) .... y_n(t) by the granule cell layer. Each output component y_i(t) is weighted by w_i, corresponding to the efficacy of the corresponding synapse between a parallel fiber and the Purkinje cell. The weighted components are summed by the Purkinje cell and constitute the filter output. The value of each weight w_i is adjusted according to the current value of the correlation between its component y_i(t) and the global retinal slip signal e(t), which arrives as climbing fiber input.

Figure 3. Performance of Model Before, During and After Training with an Undelayed Retinal-Slip Signal

The plant P is first-order filter with time constant 0.1 s, and the brainstem controller B has an undergained (50%) direct pathway and a leaky integrator (TC = 1 s) in the indirect pathway (details in Methods). (A) Eye-position response to sudden head displacement. The desired and post-training performances are effectively identical, so that only the latter is shown. (B) System gain for sinusoidal input signals as a function of frequency (Bode gain plot). Gain is measured as ratio of eye velocity amplitude to head velocity amplitude. Performance before training is shown both for the complete brainstem controller (“pre”), and for the brainstem controller as simple gain (“B = 0.5”), which corresponds to the direct pathway on its own. After training, the desired and post-training performances overlap and only the latter is shown. (C) Decline in retinal-slip amplitude with training. Root-mean-square (RMS) retinal-slip amplitudes, measured over a 5 s training batch, plotted against number of training batches. (D) Example of retinal-slip to mixed-frequency head-velocity input before and after training.

Figure 4. Model Performance Before, During, and After Training with a Retinal-Slip Signal Delayed by 0.1 s

(A) Change in retinal-slip amplitude with training. It initially declines much more slowly than with an undelayed signal (Figure 3), and eventually increases very rapidly as the system becomes unstable. (B) System gain for sinusoidal input signals as a function of frequency, measured just before the instability shown in (A). The gains at frequencies above 2.5 Hz are inaccurate. (C) Effects of delay on correlation between two identical sinusoids at 2.5 Hz. As delay increases from a value of 0 s, the correlation declines from 1.0 to 0 at a delay of 0.1 s, and to −1.0 at a delay of 0.2 s.

Figure 5. Model Performance with Delayed Retinal Slip and Frequencies >2.5 Hz Removed from Cerebellar Inputs

(A) Learning is now stable, unlike that shown in Figure 4A, but with a greater asymptotic retinal-slip error than that shown in Figure 3C. (B) System gain for sinusoidal input signals as a function of frequency. No learning occurs for frequencies above 2.5 Hz. (C) Example of retinal-slip to mixed-frequency head-velocity input before and after training. Retinal slip is still present at frequencies above 2.5 Hz.

Figure 6. Effects of Eligibility Trace on VOR Calibration

(A) Eligibility trace (blue line) used by Kettner et al. [40] and (B–D) compared to the trace required for VOR learning up to 25 Hz (green line). (B) Learning as measured by retinal slip error. (C) System gain for sinusoidal input signals as a function of frequency before and after learning. (D) Time course of retinal slip in response to colored-noise head-velocity input after learning.

Figure 7. VOR Calibration with a Second Site of Plasticity in the Brainstem

(A) Learning as measured by retinal slip error. (B) Bode gain of system before and after learning. (C) Retinal slip in response to colored-noise head velocity before and after learning. (D) Change in gain of brainstem as learning proceeds.

Figure 8. VOR Calibration with a Second Site of Plasticity in the Brainstem at 5Hz Training Frequency

(A) Learning as measured by retinal-slip error. (B) Generalization of gain to frequencies other than that used in training. Graph format chosen to resemble that of Figure 7 of Raymond and Lisberger [25]. Black disc on “post” curve indicates training frequency. (C) Gain of system as training proceeds, with or without the simulated cerebellum. The effect of cerebellar inactivation becomes smaller with longer training. (D) Output of simulated cerebellum as training proceeds. An initial fast rise from a pre-training value of 0 is succeeded by a slower fall, eventually back to 0.