A theory of attending, remembering, and reinforcement in delayed matching to sample
- PMID: 17970420
- PMCID: PMC1986439
- DOI: 10.1901/jeab.2007.88-285
A theory of attending, remembering, and reinforcement in delayed matching to sample
Erratum in
- J Exp Anal Behav. 2008 Jul;90(1):130
Abstract
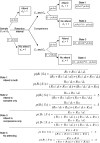
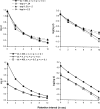
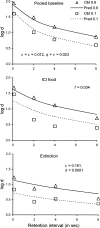
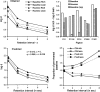
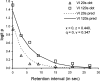
A theory of attending and reinforcement in conditional discriminations is extended to working memory in delayed matching to sample by adding terms for disruption of attending during the retention interval. Like its predecessor, the theory assumes that reinforcers and disruptors affect the independent probabilities of attending to sample and comparison stimuli in the same way as the rate of overt free-operant responding as suggested by Nevin and Grace, and that attending is translated into discriminative performance by the model of Davison and Nevin. The theory accounts for the effects of sample-stimulus discriminability and retention-interval disruption on the levels and slopes of forgetting functions, and for the diverse relations between accuracy and sensitivity to reinforcement reported in the literature. It also accounts for the effects of reinforcer probability in multiple schedules on the levels and resistance to change of forgetting functions; for the effects of reinforcer probabilities signaled within delayed-matching trials; and for the effects of reinforcer delay, sample duration, and intertrial-interval duration. The model accounts for some data that have been problematic for previous theories, and makes testably different predictions of the effects of reinforcer probabilities and disruptors on forgetting functions in multiple schedules and signaled trials.
Figures


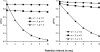

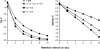

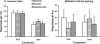


Similar articles
-
Direct remembering, mediated remembering, and atypical forgetting functions.J Exp Anal Behav. 2018 Jan;109(1):70-86. doi: 10.1002/jeab.298. Epub 2018 Jan 2. J Exp Anal Behav. 2018. PMID: 29293263
-
A theory of attending and reinforcement in conditional discriminations.J Exp Anal Behav. 2005 Sep;84(2):281-303. doi: 10.1901/jeab.2005.97-04. J Exp Anal Behav. 2005. PMID: 16262190 Free PMC article.
-
Remembering as discrimination in delayed matching to sample: discriminability and bias.Learn Behav. 2007 Aug;35(3):177-83. doi: 10.3758/bf03193053. Learn Behav. 2007. PMID: 17918423
-
A model for discriminating reinforcers in time and space.Behav Processes. 2016 Jun;127:62-73. doi: 10.1016/j.beproc.2016.03.010. Epub 2016 Mar 22. Behav Processes. 2016. PMID: 27016156 Review.
-
Acquisition of choice in concurrent chains: Assessing the cumulative decision model.Behav Processes. 2016 May;126:82-93. doi: 10.1016/j.beproc.2016.03.011. Epub 2016 Mar 19. Behav Processes. 2016. PMID: 27005579 Review.
Cited by
-
Resistance to change and relapse of observing.J Exp Anal Behav. 2012 May;97(3):281-304. doi: 10.1901/jeab.2012.97-281. J Exp Anal Behav. 2012. PMID: 22693359 Free PMC article.
-
Differential reinforcement and resistance to change of divided-attention performance.Learn Behav. 2012 Jun;40(2):158-69. doi: 10.3758/s13420-011-0052-4. Learn Behav. 2012. PMID: 22038737 Free PMC article.
-
Effects of prefeeding, extinction, and distraction during sample and comparison presentation on sensitivity to reinforcer frequency in matching to sample.Behav Processes. 2009 May;81(1):65-73. doi: 10.1016/j.beproc.2009.02.003. Epub 2009 Feb 13. Behav Processes. 2009. PMID: 19429198 Free PMC article.
-
Sensitivity of conditional-discrimination performance to within-session variation of reinforcer frequency.J Exp Anal Behav. 2008 Nov;90(3):301-11. doi: 10.1901/jeab.2008.90-301. J Exp Anal Behav. 2008. PMID: 19070338 Free PMC article.
-
Delayed matching to sample: reinforcement has opposite effects on resistance to change in two related procedures.Learn Behav. 2012 Dec;40(4):380-92. doi: 10.3758/s13420-011-0059-x. Learn Behav. 2012. PMID: 22205622 Free PMC article.
References
-
- Alling K, Nickel M, Poling A. The effects of differential and nondifferential outcomes on response rates and accuracy under a delayed-matching-to-sample procedure. The Psychological Record. 1991;41:537–549.
-
- Alsop B. Detection and choice. New Zealand: University of Auckland; 1988.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

