From inverse problems in mathematical physiology to quantitative differential diagnoses
- PMID: 17997590
- PMCID: PMC2065888
- DOI: 10.1371/journal.pcbi.0030204
From inverse problems in mathematical physiology to quantitative differential diagnoses
Erratum in
-
Correction: From Inverse Problems in Mathematical Physiology to Quantitative Differential Diagnoses.PLoS Comput Biol. 2019 Jun 24;15(6):e1007155. doi: 10.1371/journal.pcbi.1007155. eCollection 2019 Jun. PLoS Comput Biol. 2019. PMID: 31233499 Free PMC article.
Abstract
The improved capacity to acquire quantitative data in a clinical setting has generally failed to improve outcomes in acutely ill patients, suggesting a need for advances in computer-supported data interpretation and decision making. In particular, the application of mathematical models of experimentally elucidated physiological mechanisms could augment the interpretation of quantitative, patient-specific information and help to better target therapy. Yet, such models are typically complex and nonlinear, a reality that often precludes the identification of unique parameters and states of the model that best represent available data. Hypothesizing that this non-uniqueness can convey useful information, we implemented a simplified simulation of a common differential diagnostic process (hypotension in an acute care setting), using a combination of a mathematical model of the cardiovascular system, a stochastic measurement model, and Bayesian inference techniques to quantify parameter and state uncertainty. The output of this procedure is a probability density function on the space of model parameters and initial conditions for a particular patient, based on prior population information together with patient-specific clinical observations. We show that multimodal posterior probability density functions arise naturally, even when unimodal and uninformative priors are used. The peaks of these densities correspond to clinically relevant differential diagnoses and can, in the simplified simulation setting, be constrained to a single diagnosis by assimilating additional observations from dynamical interventions (e.g., fluid challenge). We conclude that the ill-posedness of the inverse problem in quantitative physiology is not merely a technical obstacle, but rather reflects clinical reality and, when addressed adequately in the solution process, provides a novel link between mathematically described physiological knowledge and the clinical concept of differential diagnoses. We outline possible steps toward translating this computational approach to the bedside, to supplement today's evidence-based medicine with a quantitatively founded model-based medicine that integrates mechanistic knowledge with patient-specific information.
Conflict of interest statement
Figures

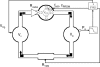
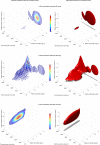
 , heart rate f
HR, and myocardial contractility c
PRSW. See text for details.
, heart rate f
HR, and myocardial contractility c
PRSW. See text for details.
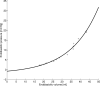
 . Simulations were performed by varying total intravascular volume between 3,000 and 8,000 ml and plotting stroke volumes versus venous pressures after 600 s of simulated time.
. Simulations were performed by varying total intravascular volume between 3,000 and 8,000 ml and plotting stroke volumes versus venous pressures after 600 s of simulated time.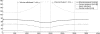
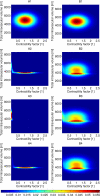
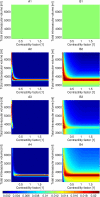

References
-
- Harvey S, Harrison DA, Singer M, Ashcroft J, Jones CM, et al. Assessment of the clinical effectiveness of pulmonary artery catheters in management of patients in intensive care (PAC-Man): a randomised controlled trial. Lancet. 2005;366:472–477. - PubMed
-
- Shah MR, Hasselblad V, Stevenson LW, Binanay C, O'Connor CM, et al. Impact of the pulmonary artery catheter in critically ill patients: meta-analysis of randomized clinical trials. JAMA. 2005;294:1664–1670. - PubMed
-
- Kulkarni AV. The challenges of evidence-based medicine: a philosophical perspective. Med Health Care Philos. 2005;8:255–260. - PubMed
-
- Doherty S. Evidence-based medicine: arguments for and against. Emerg Med Australas. 2005;17:307–313. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

