Continuous inertial focusing, ordering, and separation of particles in microchannels

Abstract

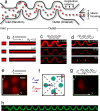
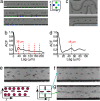
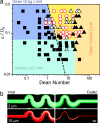
Under laminar flow conditions, when no external forces are applied, particles are generally thought to follow fluid streamlines. Contrary to this perspective, we observe that flowing particles migrate across streamlines in a continuous, predictable, and accurate manner in microchannels experiencing laminar flows. The migration is attributed to lift forces on particles that are observed when inertial aspects of the flow become significant. We identified symmetric and asymmetric channel geometries that provide additional inertial forces that bias particular equilibrium positions to create continuous streams of ordered particles precisely positioned in three spatial dimensions. We were able to order particles laterally, within the transverse plane of the channel, with >80-nm accuracy, and longitudinally, in regular chains along the direction of flow. A fourth dimension of rotational alignment was observed for discoidal red blood cells. Unexpectedly, ordering appears to be independent of particle buoyant direction, suggesting only minor centrifugal contributions. Theoretical analysis indicates the physical principles are operational over a range of channel and particle length scales. The ability to differentially order particles of different sizes, continuously, at high rates, and without external forces in microchannels is expected to have a broad range of applications in continuous bioparticle separation, high-throughput cytometry, and large-scale filtration systems.

Fig. 1.

Inertial self-ordering. (a) Schematic drawing of the inertial ordering process. After flowing through a channel of a particular symmetry, precise ordering of initially scattered particles is observed both longitudinally along the direction of flow and laterally across the channel. (b) Top-down views of fluorescent streak images of flowing 9-μm-diameter particles in a square channel (50 μm) filled with water (density ρ = 1.00 g/ml and dynamic viscosity μ = 10⁻³ Pa·s). Flow is from left to right. The inlet region is shown at the left, where the particles are initially uniformly distributed within the fluid. Longer images show the outlet 3 cm downstream for the channel Reynolds number R_c = 15, 30, or 90 (particle Reynolds number R_p = 0.48, 0.97, or 2.9). Focusing of particles into four single streamlines is observed. From above this appears as three lines with double the intensity in the middle streak–line. (c) For a symmetric curving channel the symmetry of the system reduces focusing to two streams. Above a critical Dean number (De) focusing is perturbed. (d) For an asymmetric curving system, focusing down to a single stream is favored. Focusing is again more complex as De increases. (e) A confocal cross-section of the rectangular channel shown in b shows focusing of particles to the four channel faces. (Scale bar, 10 μm.) (f) Schematic diagram showing the force balance between the shear-gradient (F_shear, red arrows) and wall-induced lift (F_wall, blue arrows) for particles in three positions. (g) Confocal cross-section for an asymmetric channel. (h) Starting at the inlet on the left, a random inlet distribution of fluorescent microparticles is focused to a tight streamline on the right after a short distance. (Scale bar, 160 μm.)

Fig. 2.

Density independence of inertial focusing. (a) Polystyrene particles (10-μm diameter, ρ = 1.05 g/ml) initially unfocused were focused when suspended in solutions of both higher and lower density (ρ = 0.78–1.23 g/ml). The R_p in this system is 0.2. (Scale bar, 50 μm.) (b) A graph showing intensity cross-sections for these focused streams indicates focusing position is not affected by relative particle density or sign. a.u., Arbitrary units. (c) Particles both more dense (polystyrene, ρ = 1.05 g/ml) and less dense (silicone oil, ρ = 0.95 g/ml) than the suspending solution focus unexpectedly to the same streamline. (Scale bar, 100 μm.)

Fig. 3.

Longitudinal and rotational inertial self-ordering. (a) Three high-speed images (2-μs exposure) are shown, demonstrating ordered particle trains at the four positions of equilibrium. Particles are 10 μm in diameter and the flow is at R_c = 120. Colored arrows below the images indicate particles at specific positions in the y–z plane that correspond to the legend. Trains tend to alternate between the positions instead of occupying several coincidently. (Scale bar, 20 μm.) (b) An autocorrelation function (ACF) confirms particle ordering with an average distance of 36 μm. (c and d) For an asymmetric curved channel, ordering occurs with a larger average displacement of 48 μm. (e) For R_c = 0.3, high-speed images of dilute whole blood show random distributions and random rotational alignment of red blood cells within a 50-μm channel. (f) At R_c = 60 a high-speed image with the focus at the midplane of the channel reveals characteristic trains of red blood cells at the top and bottom of the image. Rotational alignment of these cells is observed with the disk axis parallel to the wall. (g) Focusing at the bottom of the channel for the same R_c reveals trains of red blood cells with a similar alignment of the disk axis to the nearest wall, consistent with symmetry.

Fig. 4.

Size dependence of particle ordering. (a) Results for focusing to a single streamline as a function of the Dean number of the flow and the ratio of particle diameter to channel hydraulic diameter (a/D_h) are plotted. No focusing or focusing to four streams corresponds to filled squares, focusing to two streams corresponds to open triangles, focusing to a single stream is represented by open circles, and more complex behavior is shown as filled triangles. Data for this graph were collected by using various-sized particles and channel geometries with a fixed length of 3 cm. Different regimes for successful focusing are defined by interaction of Dean drag (F_D) and inertial lift (F_z) across the parameter space. The broken line represents a line of constant Dean drag of 0.5 nN. (b) Differential focusing of 10- and 2-μm mixed particles in water. The 2-μm particles remain unfocused after transiting 3 cm of asymmetric turns, whereas 10-μm particles are sharply focused. R_c = 7.5. (Scale bar, 50 μm.) Fractions of the stream can be collected to obtain ideally pure smaller particles and enriched populations of larger particles at high throughput.