Tensor splines for interpolation and approximation of DT-MRI with applications to segmentation of isolated rat hippocampi

Abstract

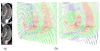
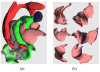
In this paper, we present novel algorithms for statistically robust interpolation and approximation of diffusion tensors-which are symmetric positive definite (SPD) matrices-and use them in developing a significant extension to an existing probabilistic algorithm for scalar field segmentation, in order to segment diffusion tensor magnetic resonance imaging (DT-MRI) datasets. Using the Riemannian metric on the space of SPD matrices, we present a novel and robust higher order (cubic) continuous tensor product of B-splines algorithm to approximate the SPD diffusion tensor fields. The resulting approximations are appropriately dubbed tensor splines. Next, we segment the diffusion tensor field by jointly estimating the label (assigned to each voxel) field, which is modeled by a Gauss Markov measure field (GMMF) and the parameters of each smooth tensor spline model representing the labeled regions. Results of interpolation, approximation, and segmentation are presented for synthetic data and real diffusion tensor fields from an isolated rat hippocampus, along with validation. We also present comparisons of our algorithms with existing methods and show significantly improved results in the presence of noise as well as outliers.

Fig. 1

(a) Tangent space of the manifold M of diffusion tensors at point p₁. The tangent vector X points to the direction of geodesic γ(t) between the points p₁ and p₂. (b) A cubic tensor spline S(t), that approximates p_is of a 1-D tensor field. The given points p_i and the points of the tensor spline S(t) are SPD matrices, elements of the Riemannian manifold M. Seven control points c_i and 11 knots t_i are required. The association between basis functions N_i,4(t), knots t_i and given data points p_i is displayed in this figure.

Fig. 2

Comparison of approximation methods using a SNR = 5.0 (top) and a SNR = 3.0 (bottom), (a) Primary eigenvectors of the noisy tensor fields. The rest of the columns shows the error in robust approximation using (b) Euclidean spline, (c) PDE interpolation, (d) log-Euclidean spline, and (e) tensor spline. The Riemannian metric was employed for computing these errors.

Fig. 3

Real DTI from an isolated rat hippocampus: (a) FA maps before (top) and after (bottom) tensor spline approximation. (b) principal eigenvector field after log-Euclidean geodesic approximation (left), and nonrobust tensor spline approximation (right).

Fig. 4

Segmentation of various synthetic tensor fields. Figures depict the estimated boundaries between regions and the corresponding primary eigenvector fields.

Fig. 5

Illustration of segmentation under partial voluming effects. Top: averaging kernels at different locations of the diffusion-weighted images. Bottom: corresponding estimated tensor fields.

Fig. 6

2-D segmentation of an isolated rat hippocampus DT-MRI: (a) FA map segmentation using algorithm in [26] (b) tensor field using piecewise constant models, (c) tensor field using a smoothly varying representation of the regions, and (d) comparison of our results (shown in the background) with a manually labeled image based on knowledge of hippocampal anatomy (shown as an overlay). The index of the labels corresponds to: 1) dorsal hippocampal commissure, 2) subiculum, 3) alveus, 4) stratum oriens, 5) stratum radiatum, 6) stratum lacunosum-moleculare, 7) molecular layer, 8) hilus, X) mixture of CA3 stratum pyramidale and stratum lucidum, Y) stratum oriens but ambiguous, 12) fimbria.

Fig. 7

(a) View of the 3-D segmentation of an isolated rat hippocampus, (b) Different views of the molecular layer from the segmentation in (a).

Algorithm 1

Intrinsic weighted mean of tensors.

Algorithm 2

Control tensors estimation.