Resolving the fast kinetics of cooperative binding: Ca2+ buffering by calretinin

Abstract

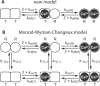
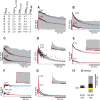
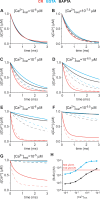
Cooperativity is one of the most important properties of molecular interactions in biological systems. It is the ability to influence ligand binding at one site of a macromolecule by previous ligand binding at another site of the same molecule. As a consequence, the affinity of the macromolecule for the ligand is either decreased (negative cooperativity) or increased (positive cooperativity). Over the last 100 years, O2 binding to hemoglobin has served as the paradigm for cooperative ligand binding and allosteric modulation, and four practical models were developed to quantitatively describe the mechanism: the Hill, the Adair-Klotz, the Monod-Wyman-Changeux, and the Koshland-Némethy-Filmer models. The predictions of these models apply under static conditions when the binding reactions are at equilibrium. However, in a physiological setting, e.g., inside a cell, the timing and dynamics of the binding events are essential. Hence, it is necessary to determine the dynamic properties of cooperative binding to fully understand the physiological implications of cooperativity. To date, the Monod-Wyman-Changeux model was applied to determine the kinetics of cooperative binding to biologically active molecules. In this model, cooperativity is established by postulating two allosteric isoforms with different binding properties. However, these studies were limited to special cases, where transition rates between allosteric isoforms are much slower than the binding rates or where binding and unbinding rates could be measured independently. For all other cases, the complex mathematical description precludes straightforward interpretations. Here, we report on calculating for the first time the fast dynamics of a cooperative binding process, the binding of Ca2+ to calretinin. Calretinin is a Ca2+-binding protein with four cooperative binding sites and one independent binding site. The Ca2+ binding to calretinin was assessed by measuring the decay of free Ca2+ using a fast fluorescent Ca2+ indicator following rapid (<50-mus rise time) Ca2+ concentration jumps induced by uncaging Ca2+ from DM-nitrophen. To unravel the kinetics of cooperative binding, we devised several approaches based on known cooperative binding models, resulting in a novel and relatively simple model. This model revealed unexpected and highly specific nonlinear properties of cellular Ca2+ regulation by calretinin. The association rate of Ca2+ with calretinin speeds up as the free Ca2+ concentration increases from cytoplasmic resting conditions ( approximately 100 nM) to approximately 1 muM. As a consequence, the Ca2+ buffering speed of calretinin highly depends on the prevailing Ca2+ concentration prior to a perturbation. In addition to providing a novel mode of action of cellular Ca2+ buffering, our model extends the analysis of cooperativity beyond the static steady-state condition, providing a powerful tool for the investigation of the dynamics and functional significance of cooperative binding in general.

Figure 1. Ca²⁺ Measurements In Vitro

(A) Examples of changes in free [Ca²⁺] after photolysis of DMn in the absence of protein (upper trace) and in the presence of 31 μM and 62 μM CR (middle and lower traces, respectively). The UV flash energies used to uncage DMn were of similar magnitude, resulting in an equivalent amount of uncaged Ca²⁺. (B) Scheme of all equilibrium reactions occurring in the measurement chamber after photolysis of caged Ca²⁺. The kinetic rate constants for DMn, its photoproducts (PP), and the Oregon Green BAPTA 5N (OGB-5N), and uncaging time constants (τ_f and τ_s) of DMn were independently determined. The reaction parameters to be determined for describing the Ca²⁺ binding to CR are indicated by a question mark (?).

Figure 2. Models Used to Simulate Cooperativity

Both models used to simulate cooperativity are based on the ability of the binding sites to occur in two states, one with a low affinity for Ca²⁺ (T) and one with a high affinity (R). In the new model (A), a binding site is in the T state when the other binding site has no Ca²⁺ bound, and it is in the R state when the other site has Ca²⁺ bound. In this model, the transitions from T to R and vice versa are considered to occur instantaneously. In the MWC model, the cooperative pair of binding sites are either both in the T state or both in the R state. The transitions between R and T occur according to the transition constants k ₊ and k ₋. For each occupation level, there is a separate equilibrium (L ₀, L ₁, and L ₂) for which it can be shown that under specific conditions, the equilibrium shifts from mainly the T state in the unoccupied cooperative sets to mainly the R state in fully occupied states (see also Equations 8, 9, and 10).

Figure 3. Fitting of the Ca²⁺ Uncaging Data with the Model of Two Pairs of Cooperative Sites and One Individual Site

A typical dataset (•) consisting of 14 randomly chosen traces is shown in (A–G). The traces were selected from seven different experimental conditions, two per condition. The table shows the values for the four variables differing in conditions (A–G). Individual data points (•) are fitted with either the new model (red lines) or the MWC model (blue lines), taking into consideration the four variables listed in the table, whereas the values for k _on's, k _off's, K _d(app), L ₀, k _+(L0), and the n _H for CR are identical for all fits within a set. The amount of uncaging is fitted independently for every trace. For the selected examples, it is expressed as percentage of total [DMn]. The gray areas indicate the whole range of uncaging experiments for each experimental condition; the smaller insets in (D–G) show the whole range of traces, whereas the y-axis ranges in the main panels (D–G) were selected to optimally show the 14 selected traces. More individual curves can be seen in Figure S1. Black scale bars in (A–G) insets indicate 50% ΔF/F (y-axis) or 20 ms (x-axis). (H) To assess the goodness of fit by the new model, the averaged relative deviations of the fit from the data are shown as black bars ± the standard error of the mean for the first 20 ms of the fit (left) and for 20–50 ms of the fit (right bar). The largest single deviations in either direction found in all of the sets are indicated by striped bars. The yellow bars indicate the deviation observed in the selected set of traces displayed in (A–G). The scale bar indicates 5% error/deviation from data. In the table for the OGB-5N column, I refers to lot number 34B1–2 and II to lot 15C1–2.

Figure 4. Properties of the Independent Site

The 38 fit results for the k _on's, k _off's (B), and K _d's (A) of the independent site (V) have a log-normal distribution for both models. This can be seen when the data of the new model (red symbols) and the MWC model (blue symbols) are plotted on a logarithmic scale as a cumulative probability plot. The k _on's, k _off's (B), and, k _d's (A) were fitted (solid lines) with a single log-normal function, indicating a uniform result for the 38 fits. The yellow symbols are derived from the dataset shown in Figure 3.

Figure 5. Properties of the Cooperative Sites

The data of the 38 fit results for the rate and affinity constants have a log-normal distribution, evidenced when plotted on a logarithmic scale as a cumulative probability (A–D). All data could be fitted (solid lines) with a single log-normal function, indicating a unique result for the 38 fits. The Hill coefficient for both models was normally distributed (E) and was fitted accordingly. In all subfigures (A–E), red symbols indicate results for fits with the new model and blue symbols indicate results for the fits with the MWC model. The values for the dissociation constants in (A) and the rate constants in (B) found for the T state are indicated by open squares (□), whereas the values for the R state are indicated with closed circles (•). The arrows indicate the general shift from T state to R state as the cooperative sites bind Ca²⁺. The apparent dissociation constants (A) are indicated with pink circles for the new model and green circles for the MWC model. The equilibrium constants and rate constants for the transition from the T to the R state in the MWC model are shown in (C) and (D), respectively. The Hill coefficients obtained are shown in (E). The yellow symbols are the data points derived from the experiment shown in Figure 3.

Figure 6. Transfer Function of CR

The transfer functions for 500 μM CR simulated with either the new model (A) or the MWC model (B). The transfer functions for 500 μM CR were determined by simulating a 1 nM fluctuation in [Ca²⁺] at different frequencies and various resting [Ca²⁺]. The output was determined from the peak-to-peak amplitude of the resulting Ca²⁺ waveform.

Figure 7. Kinetic Behavior of CR Determined with the Nonlinear Kinetic Parameters

The graphs represent simulated Ca²⁺ signals induced by 1 μM steps in [Ca²⁺] in the presence of 100 μM CR (red lines), 153 μM EGTA (blue lines), or 7.8 μM BAPTA (black lines). (A) The simulated Ca²⁺ signal induced by a 1 μM step in [Ca²⁺] from a starting [Ca²⁺] of 10 nM in the presence of 100 μM CR resulted in the red [Ca²⁺] decay curve. This trace was used to model the concentrations of EGTA or BAPTA needed to best fit the CR [Ca²⁺] decay curve, and were found to be either 153 μM (EGTA; blue trace) or 7.8 μM (BAPTA; black trace). (B–G) The same step in [Ca²⁺] of 1 μM was then “induced” from increasing resting [Ca²⁺](solid lines). The [Ca²⁺] decay curves from the previous image (lower resting [Ca²⁺]) were depicted as dashed lines (e.g., the dashed lines in [C] are the solid lines from [B]) to highlight the “shift” of the curves as the resting [Ca²⁺] increases. If the solid line is below the dashed line of the same color, the [Ca²⁺] decay becomes faster, and vice versa, a solid line above the dashed line indicates a slowing of the [Ca²⁺] decay. The decay in the presence of CR (red) becomes faster when the starting [Ca²⁺] increases from 10 nM to 1 μM (A–E) and then slows down from 1 μM to 10 μM. (H) shows the concentration of either EGTA (blue) or BAPTA (black) needed to mimic the buffering of a 1 μM step in [Ca²⁺] by 100 μM CR at different resting [Ca²⁺]. The intercept between the red line with the blue and black curves indicate at what starting [Ca²⁺] the synthetic buffers closely mimic a 1 μM step in [Ca²⁺] in the presence of 100 μM CR. Note that since CR has five Ca²⁺-binding sites and EGTA and BAPTA only one each, 100 μM CR was considered to be equivalent to 500 μM EGTA or BAPTA. Thus, for the selected 1 μM step in [Ca²⁺] at a lower starting [Ca²⁺] (approximately 100 nM), CR apparently behaves more like EGTA, whereas at higher starting [Ca²⁺] (>3 μM), CR works more like BAPTA.