On the relationship between thermal stability and catalytic power of enzymes
- PMID: 18052079
- PMCID: PMC3174049
- DOI: 10.1021/bi701732a
On the relationship between thermal stability and catalytic power of enzymes
Abstract
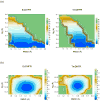
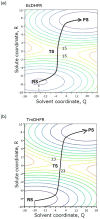
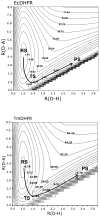
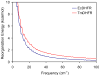
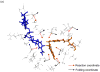
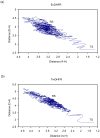
The possible relationship between the thermal stability and the catalytic power of enzymes is of great current interest. In particular, it has been suggested that thermophilic or hyperthermophilic (Tm) enzymes have lower catalytic power at a given temperature than the corresponding mesophilic (Ms) enzymes, because the thermophilic enzymes are less flexible (assuming that flexibility and catalysis are directly correlated). These suggestions presume that the reduced dynamics of the thermophilic enzymes is the reason for their reduced catalytic power. The present paper takes the specific case of dihydrofolate reductase (DHFR) and explores the validity of the above argument by simulation approaches. It is found that the Tm enzymes have restricted motions in the direction of the folding coordinate, but this is not relevant to the chemical process, since the motions along the reaction coordinate are perpendicular to the folding motions. Moreover, it is shown that the rate of the chemical reaction is determined by the activation barrier and the corresponding reorganization energy, rather than by dynamics or flexibility in the ground state. In fact, as far as flexibility is concerned, we conclude that the displacement along the reaction coordinate is larger in the Tm enzyme than in the Ms enzyme and that the general trend in enzyme catalysis is that the best catalyst involves less motion during the reaction than the less optimal catalyst. The relationship between thermal stability and catalysis appears to reflect the fact that to obtain small electrostatic reorganization energy it is necessary to invest some folding energy in the overall preorganization process. Thus, the optimized catalysts are less stable. This trend is clearly observed in the DHFR case.
Figures
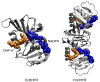





References
-
- Marti S, Roca M, Andres J, Moliner V, Silla E, Tunon I, Bertran J. Theoretical insights in enzyme catalysis. Chemical Society Reviews. 2004;33:98–107. - PubMed
-
- Warshel A, Sharma PK, Kato M, Xiang Y, Liu HB, Olsson MHM. Electrostatic basis for enzyme catalysis. Chemical Reviews. 2006;106:3210–3235. - PubMed
-
- Epstein DM, Benkovic SJ, Wright PE. Dynamics of the Dihydrofolate-Reductase Folate Complex - Catalytic Sites and Regions Known to Undergo Conformational Change Exhibit Diverse Dynamical Features. Biochemistry. 1995;34:11037–11048. - PubMed
-
- Schnell JR, Dyson HJ, Wright PE. Structure, dynamics, and catalytic function of dihydrofolate reductase. Annual Review of Biophysics and Biomolecular Structure. 2004;33:119–140. - PubMed
-
- Hammes-Schiffer S. Quantum-classical simulation methods for hydrogen transfer in enzymes: a case study of dihydrofolate reductase. Current Opinion in Structural Biology. 2004;14:192–201. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

