Review on solving the forward problem in EEG source analysis
- PMID: 18053144
- PMCID: PMC2234413
- DOI: 10.1186/1743-0003-4-46
Review on solving the forward problem in EEG source analysis
Abstract
Background: The aim of electroencephalogram (EEG) source localization is to find the brain areas responsible for EEG waves of interest. It consists of solving forward and inverse problems. The forward problem is solved by starting from a given electrical source and calculating the potentials at the electrodes. These evaluations are necessary to solve the inverse problem which is defined as finding brain sources which are responsible for the measured potentials at the EEG electrodes.
Methods: While other reviews give an extensive summary of the both forward and inverse problem, this review article focuses on different aspects of solving the forward problem and it is intended for newcomers in this research field.
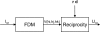
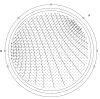
Results: It starts with focusing on the generators of the EEG: the post-synaptic potentials in the apical dendrites of pyramidal neurons. These cells generate an extracellular current which can be modeled by Poisson's differential equation, and Neumann and Dirichlet boundary conditions. The compartments in which these currents flow can be anisotropic (e.g. skull and white matter). In a three-shell spherical head model an analytical expression exists to solve the forward problem. During the last two decades researchers have tried to solve Poisson's equation in a realistically shaped head model obtained from 3D medical images, which requires numerical methods. The following methods are compared with each other: the boundary element method (BEM), the finite element method (FEM) and the finite difference method (FDM). In the last two methods anisotropic conducting compartments can conveniently be introduced. Then the focus will be set on the use of reciprocity in EEG source localization. It is introduced to speed up the forward calculations which are here performed for each electrode position rather than for each dipole position. Solving Poisson's equation utilizing FEM and FDM corresponds to solving a large sparse linear system. Iterative methods are required to solve these sparse linear systems. The following iterative methods are discussed: successive over-relaxation, conjugate gradients method and algebraic multigrid method.
Conclusion: Solving the forward problem has been well documented in the past decades. In the past simplified spherical head models are used, whereas nowadays a combination of imaging modalities are used to accurately describe the geometry of the head model. Efforts have been done on realistically describing the shape of the head model, as well as the heterogenity of the tissue types and realistically determining the conductivity. However, the determination and validation of the in vivo conductivity values is still an important topic in this field. In addition, more studies have to be done on the influence of all the parameters of the head model and of the numerical techniques on the solution of the forward problem.
Figures










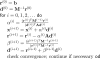
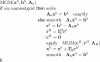
References
-
- Berger H. Über das Elektroenkephalogramm des Menschen. Archiv für Psychiatrie und Nervenkrankheiten. 1929;87:527–570. doi: 10.1007/BF01797193. - DOI
-
- Niedermeyer E, Lopes Da Silva F. Electroencephalography. Baltimore: Williams and Wilkins; 1993.
-
- Baillet S, Mosher JC, Leahy RM. Electromagnetic Brain Mapping. IEEE Signal Processing Magazine. 2001;November:14–30. doi: 10.1109/79.962275. - DOI
-
- Kiloh LG, Mc Comas AJ, Osselton JW, Upton ARM. Clinical Electroencephalography. Butterworths; 1981.
-
- Gray H. Gray's Anatomy. Longman Group Ltd; 1973.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

