Cytoskeletal bundle mechanics
- PMID: 18055529
- PMCID: PMC2275675
- DOI: 10.1529/biophysj.107.119743
Cytoskeletal bundle mechanics
Abstract
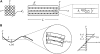
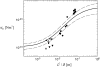
The mechanical properties of cytoskeletal actin bundles play an essential role in numerous physiological processes, including hearing, fertilization, cell migration, and growth. Cells employ a multitude of actin-binding proteins to actively regulate bundle dimensions and cross-linking properties to suit biological function. The mechanical properties of actin bundles vary by orders of magnitude depending on diameter and length, cross-linking protein type and concentration, and constituent filament properties. Despite their importance to cell function, the molecular design principles responsible for this mechanical behavior remain unknown. Here, we examine the mechanics of cytoskeletal bundles using a molecular-based model that accounts for the discrete nature of constituent actin filaments and their distinct cross-linking proteins. A generic competition between filament stretching and cross-link shearing determines three markedly different regimes of mechanical response that are delineated by the relative values of two simple design parameters, revealing the universal nature of bundle-bending mechanics. In each regime, bundle-bending stiffness displays distinct scaling behavior with respect to bundle dimensions and molecular composition, as observed in reconstituted actin bundles in vitro. This mechanical behavior has direct implications on the physiological bending, buckling, and entropic stretching behavior of cytoskeletal processes, as well as reconstituted actin systems. Results are used to predict the bending regimes of various in vivo cytoskeletal bundles that are not easily accessible to experiment and to generate hypotheses regarding implications of the isolated behavior on in vivo bundle function.
Figures

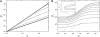

References
-
- Lodish, H., A. Berk, S. L. Zipursky, P. Matsudaira, D. Baltimore, and J. Darnell. 1999. Molecular Cell Biology. W.H. Freeman and Company, New York.
-
- Revenu, C., R. Athman, S. Robine, and D. Louvard. 2004. The co-workers of actin filaments: from cell structures to signals. Nat. Rev. Mol. Cell Biol. 5:635–646. - PubMed
-
- Kachar, B., W. E. Brownell, R. Altschuler, and J. Fex. 1986. Electrokinetic shape changes of cochlear outer hair cells. Nature. 322:365–368. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

