Threshold-dominated regulation hides genetic variation in gene expression networks

Abstract

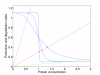
Background: In dynamical models with feedback and sigmoidal response functions, some or all variables have thresholds around which they regulate themselves or other variables. A mathematical analysis has shown that when the dose-response functions approach binary or on/off responses, any variable with an equilibrium value close to one of its thresholds is very robust to parameter perturbations of a homeostatic state. We denote this threshold robustness. To check the empirical relevance of this phenomenon with response function steepnesses ranging from a near on/off response down to Michaelis-Menten conditions, we have performed a simulation study to investigate the degree of threshold robustness in models for a three-gene system with one downstream gene, using several logical input gates, but excluding models with positive feedback to avoid multistationarity. Varying parameter values representing functional genetic variation, we have analysed the coefficient of variation (CV) of the gene product concentrations in the stable state for the regulating genes in absolute terms and compared to the CV for the unregulating downstream gene. The sigmoidal or binary dose-response functions in these models can be considered as phenomenological models of the aggregated effects on protein or mRNA expression rates of all cellular reactions involved in gene expression.

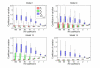
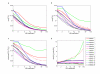
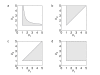
Results: For all the models, threshold robustness increases with increasing response steepness. The CVs of the regulating genes are significantly smaller than for the unregulating gene, in particular for steep responses. The effect becomes less prominent as steepnesses approach Michaelis-Menten conditions. If the parameter perturbation shifts the equilibrium value too far away from threshold, the gene product is no longer an effective regulator and robustness is lost. Threshold robustness arises when a variable is an active regulator around its threshold, and this function is maintained by the feedback loop that the regulator necessarily takes part in and also is regulated by. In the present study all feedback loops are negative, and our results suggest that threshold robustness is maintained by negative feedback which necessarily exists in the homeostatic state.

Conclusion: Threshold robustness of a variable can be seen as its ability to maintain an active regulation around its threshold in a homeostatic state despite external perturbations. The feedback loop that the system necessarily possesses in this state, ensures that the robust variable is itself regulated and kept close to its threshold. Our results suggest that threshold regulation is a generic phenomenon in feedback-regulated networks with sigmoidal response functions, at least when there is no positive feedback. Threshold robustness in gene regulatory networks illustrates that hidden genetic variation can be explained by systemic properties of the genotype-phenotype map.

Figure 1

Regulatory functions used in the simulations. (a) The Hill function describes the dose-responce relationship between the amount of a regulator x₁ and the relative production rate of the regulated gene. The threshold parameter θ₁ = 2 is the same for all four curves. (b) Regulatory function for two regulators x₁ and x₂. Two Hill functions are combined by the algebraic equivalent of the Boolean AND function (see Table 1). The parameter values used in this panel are θ₁ = θ₂ = 2 and p = 10.

Figure 2

Graphical solution of the equilibrium condition of Eq. (2) for varying steepness of the response function and varying relative degradation rates. The blue curves are graphs of r + α(1 - Z), the straight lines graph the degradation term γy. For intermediate values of γ the equilibrium concentration is close to θ and approaches θ when the response function steepness increases (red line), and there is active regulation. When γ is small, the basal transcription rate is sufficient to balance the degradation, and y* gets large (green line). When γ is large, degradation is so rapid that the protein concentration never reaches the level where it regulates. Maximal production is necessary to balance the degradation (magenta line).

Figure 3

Connectivity diagrams for the 14 network models in the simulation study. Genes 1 and 2 are represented by circles, the downstream gene 3 being omitted for clarity. The sign of an arrow indicates whether the type of regulation is activation (+), in which case the input variable is Z_i, or inhibition (-), in which case the input variable is 1 - Z_i. When a gene has two regulators, the individual signals are combined with a logic block, represented by a rectangle, merging the two signals into one by the continuous analogue of the Boolean functions AND or OR. (See the Methods section for explanations of the Boolean variables and functions.)

Figure 4

Variation in steady state values for Models 1, 9, 12, and 14. Boxplots show the distributions of the 81 coefficients of variance for all three genes using seven different Hill coefficients ranging from p = 1 to p = 100. For each Hill coefficients the three plots show from left to right the coefficient of variation for gene 1 (red), 2 (green), and 3 (blue), respectively. The boxes show the quartiles and the median. The black vertical lines extend to the largest observation and the smallest. The long black horisontal line shows the coefficient of variation 0.288 of the perturbed production rates α_j.

Figure 5

The coefficient of variation as function of the Hill coefficient for the most robust parameter sets for gene 1 and 2 across all 14 models. (a)-(b): Minimum of CV₁^k and CV₂^k, respectively, over all 81 parameter sets. (c): CV_minmax as function of the Hill coefficient for each of the 14 models. An explanation for the remarkably high values for Models 1, 2, and 11 for high Hill coefficient values is given in the text. (d) The ratio of minimum of CV₂^k to minimum of CV₁^k as function of the Hill coefficient for each of the 14 models.

Figure 6

The shaded areas are the robustness domains Ω_SSP in the (μ₁, μ₂)-plane for (a) Models 1, 2, 11, (b) Models 3, 13, (c) Model 6, (d) Models 4, 5, 7–10, 12, 14. For parameter values in Ω_SSP both x1∗ MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemiEaG3aa0baaSqaaiabigdaXaqaaiabgEHiQaaaaaa@2F58@ and x2∗ MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemiEaG3aa0baaSqaaiabikdaYaqaaiabgEHiQaaaaaa@2F5A@ are singular variables and approach their threshold values in the step function limit. Then they exhibit threshold robustness for all parameter perturbations which leave the perturbed values inside Ω_SSP.

Figure 7

In the case of very steep sigmoids, the (μ₁, μ₂) space of Model 2 is divided into 5 domains, each domain comprising the parameter values giving a particular type of SSP. For example, in the domain denoted (Z₁, 1), x₁ is at its threshold and is singular, thus Z₁ ≠ 0, 1, while x₂ is above its threshold, thus Z₂ = 1. Only in the shaded domain are both variables singular and actively regulating. For steep, but not infinitely steep response functions the relations are approximately true.