Effects of imperfect dynamic clamp: computational and experimental results

Abstract

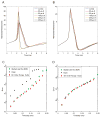
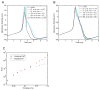
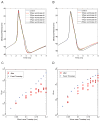
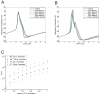
In the dynamic clamp technique, a typically nonlinear feedback system delivers electrical current to an excitable cell that represents the actions of "virtual" ion channels (e.g., channels that are gated by local membrane potential or by electrical activity in neighboring biological or virtual neurons). Since the conception of this technique, there have been a number of different implementations of dynamic clamp systems, each with differing levels of flexibility and performance. Embedded hardware-based systems typically offer feedback that is very fast and precisely timed, but these systems are often expensive and sometimes inflexible. PC-based systems, on the other hand, allow the user to write software that defines an arbitrarily complex feedback system, but real-time performance in PC-based systems can be deteriorated by imperfect real-time performance. Here, we systematically evaluate the performance requirements for artificial dynamic clamp knock-in of transient sodium and delayed rectifier potassium conductances. Specifically, we examine the effects of controller time step duration, differential equation integration method, jitter (variability in time step), and latency (the time lag from reading inputs to updating outputs). Each of these control system flaws is artificially introduced in both simulated and real dynamic clamp experiments. We demonstrate that each of these errors affect dynamic clamp accuracy in a way that depends on the time constants and stiffness of the differential equations being solved. In simulations, time steps above 0.2ms lead to catastrophic alteration of spike shape, but the frequency-current relationship is much more robust. Latency (the part of the time step that occurs between measuring membrane potential and injecting re-calculated membrane current) is a crucial factor as well. Experimental data are substantially more sensitive to inaccuracies than simulated data.

Figure 1. Dynamic clamp feedback loop

This schematic representation of a dynamic clamp system illustrates the feedback controller which measures membrane voltage, calculates a current to apply based on the dynamics of the simulated conductance, and feeds that current back to the cell. Typically the membrane voltage and applied current are conducted through the same electrode.

Figure 2. Accuracy of dynamic clamp simulations with different numerical solvers

A: Traces of simulated evoked action potentials. In this case, Na⁺ channels were simulated using the Euler method at the time step indicated in the legend. K⁺ channels and integration of the membrane equation were performed in high-precision using the NDF solver (see Methods). B: Traces of simulated action potentials in which K⁺ channels were virtualized at a given time step using the Euler method, with other elements integrated with high precision. C: Plots of error vs. time step for three methods of Na⁺ channel virtualization. Error (units of V²) is much larger for the Euler method than for the NDF or Runge-Kutta methods. D: Error vs. time step for virtualization of K⁺ channels. Accuracy is relatively independent of the solver method.

Figure 3. Effects of time step on dynamic clamp accuracy

In separate simulations Na⁺ (A) and K⁺ (B) channels were virtualized at a given time step using the 4^th-order Runge-Kutta solver. Generally, large time steps lead to massive distortions when Na⁺ channels are virtualized (A); virtualization of K⁺ channels leads to more subtle distortions, mainly by increasing the spike afterhyperpolarization. C: Summary data showing error (V²) vs. time step for the two cases.

Figure 4. Effects of time-step jitter on dynamic clamp accuracy

In these simulations, Na⁺ (A, C) and K⁺ (B, D) channels were virtualized at a time step that varied randomly from 25μs to a given worst-case value. As shown in individual traces (A–B) and summary data (C–D), error is bounded above by the worst-case time step.

Figure 5. Effects of system latency on dynamic clamp accuracy

In experiments involving virtual Na⁺ (A) and K⁺ (B) channels, we introduced latency in experiments conducted with a time step of 100μ. C: Summary data from manipulations of latency. For a given time step, the latency makes a substantial difference in the level of error.

Figure 6. Effects of time step and latency on firing rate in dynamic clamp simulations

Plots show firing rate vs. applied current for virtualized Na⁺ (A, C) and K⁺ (B, D) channels. In general, effects on firing rate were less dramatic than those on spike shape (Figs. 3, 5).

Figure 7. Whole-cell patch-clamp recordings demonstrate the effects of time step (T_s) and latency under real-world conditions

In measurements from CA1 pyramidal cells, we recorded action potentials under control conditions (A) and with virtualized Na⁺ channels (B). We also introduced long time steps (C) and latencies (D). Effects in experiments were qualitatively similar to those in simulations, but experimental data were more sensitive to inaccuracies than were simulated data from previous figures.