Sparse inverse covariance estimation with the graphical lasso

Abstract

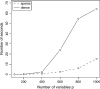
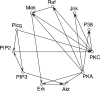
We consider the problem of estimating sparse graphs by a lasso penalty applied to the inverse covariance matrix. Using a coordinate descent procedure for the lasso, we develop a simple algorithm--the graphical lasso--that is remarkably fast: It solves a 1000-node problem ( approximately 500,000 parameters) in at most a minute and is 30-4000 times faster than competing methods. It also provides a conceptual link between the exact problem and the approximation suggested by Meinshausen and Bühlmann (2006). We illustrate the method on some cell-signaling data from proteomics.

Fig. 1.

Number of CPU seconds required for the graphical lasso procedure.

Fig. 2.

Directed acylic graph from cell-signaling data, from Sachs and others (2003).

Fig. 3.

Cell-signaling data: Undirected graphs from graphical lasso with different values of the penalty parameter ρ.

Fig. 4.

Cell-signaling data: Profile of coefficients as the total L₁norm of the coefficient vector increases, that is as ρdecreases. Profiles for the largest coefficients are labeled with the corresponding pair of proteins.

Fig. 5.

Cell-signaling data. Left panel shows 10-fold cross-validation using both regression and likelihood approaches (details in text). Right panel compares the regression sum of squares of the exact graphical lasso approach to the Meinhausen–Buhlmann approximation.