Basic math in monkeys and college students
- PMID: 18092890
- PMCID: PMC2140091
- DOI: 10.1371/journal.pbio.0050328
Basic math in monkeys and college students
Abstract
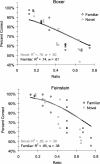
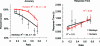
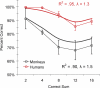
Adult humans possess a sophisticated repertoire of mathematical faculties. Many of these capacities are rooted in symbolic language and are therefore unlikely to be shared with nonhuman animals. However, a subset of these skills is shared with other animals, and this set is considered a cognitive vestige of our common evolutionary history. Current evidence indicates that humans and nonhuman animals share a core set of abilities for representing and comparing approximate numerosities nonverbally; however, it remains unclear whether nonhuman animals can perform approximate mental arithmetic. Here we show that monkeys can mentally add the numerical values of two sets of objects and choose a visual array that roughly corresponds to the arithmetic sum of these two sets. Furthermore, monkeys' performance during these calculations adheres to the same pattern as humans tested on the same nonverbal addition task. Our data demonstrate that nonverbal arithmetic is not unique to humans but is instead part of an evolutionarily primitive system for mathematical thinking shared by monkeys.
Conflict of interest statement
Figures


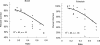
References
-
- Dehaene S. Varieties of numerical abilities. Cognition. 1992;44:1–42. - PubMed
-
- Brannon EM. What animals know about number. In: Campbell JID, editor. Handbook of mathematical cognition. New York: Psychology Press; 2005. pp. 85–108.
-
- Hauser MD, Spelke E. Evolutionary and developmental foundations of human knowledge: A case study of mathematics. In: Gazzaniga MD, editor. The cognitive neurosciences Cambridge (Massachusetts) MIT Press; 2004. pp. 853–864.
-
- Pica P, Lemer C, Izard W, Dehaene S. Exact and approximate arithmetic in an Amazonian indigene group. Science. 2004;306:499–503. - PubMed
-
- Dehaene S. The number sense: how the mind creates mathematics. New York: Oxford University Press; 1997.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

