Operating regimes of signaling cycles: statics, dynamics, and noise filtering
- PMID: 18159939
- PMCID: PMC2230677
- DOI: 10.1371/journal.pcbi.0030246
Operating regimes of signaling cycles: statics, dynamics, and noise filtering
Abstract
A ubiquitous building block of signaling pathways is a cycle of covalent modification (e.g., phosphorylation and dephosphorylation in MAPK cascades). Our paper explores the kind of information processing and filtering that can be accomplished by this simple biochemical circuit. Signaling cycles are particularly known for exhibiting a highly sigmoidal (ultrasensitive) input-output characteristic in a certain steady-state regime. Here, we systematically study the cycle's steady-state behavior and its response to time-varying stimuli. We demonstrate that the cycle can actually operate in four different regimes, each with its specific input-output characteristics. These results are obtained using the total quasi-steady-state approximation, which is more generally valid than the typically used Michaelis-Menten approximation for enzymatic reactions. We invoke experimental data that suggest the possibility of signaling cycles operating in one of the new regimes. We then consider the cycle's dynamic behavior, which has so far been relatively neglected. We demonstrate that the intrinsic architecture of the cycles makes them act--in all four regimes--as tunable low-pass filters, filtering out high-frequency fluctuations or noise in signals and environmental cues. Moreover, the cutoff frequency can be adjusted by the cell. Numerical simulations show that our analytical results hold well even for noise of large amplitude. We suggest that noise filtering and tunability make signaling cycles versatile components of more elaborate cell-signaling pathways.
Conflict of interest statement
Figures

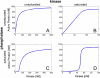
 , a
1 = 1, K
1 = 10,000, a
2 = 1,
, a
1 = 1, K
1 = 10,000, a
2 = 1, , K
2 = 10,000, k
1 = 1, and k
2 = 1, where all reaction rates are in units of 1/s, concentrations and Michaelis constants are in nanomoles, and second-order reaction rates (a
1 and a
2) are in 1/nM/s. (B) When the kinase is saturated and the phosphatase unsaturated, a linear response results. The parameters here are
, K
2 = 10,000, k
1 = 1, and k
2 = 1, where all reaction rates are in units of 1/s, concentrations and Michaelis constants are in nanomoles, and second-order reaction rates (a
1 and a
2) are in 1/nM/s. (B) When the kinase is saturated and the phosphatase unsaturated, a linear response results. The parameters here are  , a
1 = 100, K
1 = 10, a
2 = 1,
, a
1 = 100, K
1 = 10, a
2 = 1,  , K
2 = 10,000, k
1 = 500, and k
2 = 10,000. (C) When the kinase is unsaturated and the phosphatase saturated, a threshold-hyperbolic response results. The parameters for this cycle are
, K
2 = 10,000, k
1 = 500, and k
2 = 10,000. (C) When the kinase is unsaturated and the phosphatase saturated, a threshold-hyperbolic response results. The parameters for this cycle are  , a
1 = 100, K
1 = 10,000, a
2 = 100,
, a
1 = 100, K
1 = 10,000, a
2 = 100,  , K
2 = 1, k
1 = 25, and k
2 = 1. (D) When both enzymes are saturated, an ultrasensitive response results. The parameters used for this cycle are
, K
2 = 1, k
1 = 25, and k
2 = 1. (D) When both enzymes are saturated, an ultrasensitive response results. The parameters used for this cycle are  , a
1 = 100, K
1 = 10, a
2 = 100,
, a
1 = 100, K
1 = 10, a
2 = 100,  , K
2 = 10, k
1 = 1, and k
2 = 1. The parameters for the four cycles were chosen to be comparable in magnitude to values found in the literature (see [11,62], for example).
, K
2 = 10, k
1 = 1, and k
2 = 1. The parameters for the four cycles were chosen to be comparable in magnitude to values found in the literature (see [11,62], for example).
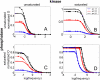
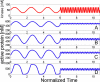

References
-
- Rao CV, Arkin AP. Control motifs for intracellular regulatory networks. Annu Rev Biomed Eng. 2001;3:391–419. - PubMed
-
- Sauro HM, Kholodenko BN. Quantitative analysis of signaling networks. Prog Biophys Mol Biol. 2004;86:5–43. - PubMed
-
- Wiley HS, Shvartsman SY, Lauffenburger DA. Computational modeling of the egf-receptor system: a paradigm for systems biology. Trends Cell Biol. 2003;13:43–50. - PubMed
-
- Li C, Ge QW, Nakata M, Matsuno H, Miyano S. Modelling and simulation of signal transductions in an apoptosis pathway by using timed Petri nets. J Biosci. 2007;32:113–127. - PubMed
Publication types
MeSH terms
Substances
Associated data
- Actions
- Actions
- Actions
- Actions
- Actions
- Actions
- Actions
- Actions
Grants and funding
LinkOut - more resources
Full Text Sources

