Anomalous dynamics of cell migration

Abstract

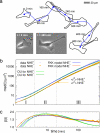
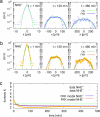
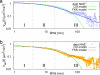
Cell movement--for example, during embryogenesis or tumor metastasis--is a complex dynamical process resulting from an intricate interplay of multiple components of the cellular migration machinery. At first sight, the paths of migrating cells resemble those of thermally driven Brownian particles. However, cell migration is an active biological process putting a characterization in terms of normal Brownian motion into question. By analyzing the trajectories of wild-type and mutated epithelial (transformed Madin-Darby canine kidney) cells, we show experimentally that anomalous dynamics characterizes cell migration. A superdiffusive increase of the mean squared displacement, non-Gaussian spatial probability distributions, and power-law decays of the velocity autocorrelations is the basis for this interpretation. Almost all results can be explained with a fractional Klein-Kramers equation allowing the quantitative classification of cell migration by a few parameters. Thereby, it discloses the influence and relative importance of individual components of the cellular migration apparatus to the behavior of the cell as a whole.

Fig. 1.

Summary of migration experiments. (a) Overlay of a migrating MDCK-F NHE⁺ cell with its path covered within 480 min. The cell frequently changes its shape and direction during migration. (b) Double-logarithmic plot of the mean squared displacement (msd) as a function of time. Experimental data points for both cell types are symbolized by triangles and circles. Different time scales are marked as phases I, II, and III as discussed in the text. The solid blue and orange lines represent the fit to the msd of the fractional Klein–Kramers (FKK) equation including a noise term (Eq. 10). Green lines show the results of the Ornstein–Uhlenbeck (OU) model plus noise (Eq. 11). The corresponding parameters of the theoretical models are given in Tables 1 and 2. The dashed black lines indicate the uncertainties of the msd values according to Eq. 15. (c) Logarithmic derivative β(t) (Eq. 2) of the msd for MDCK-F NHE⁺ and NHE⁻ cells. Data and model curves are marked as in b.

Fig. 2.

Time-dependent development of the spatial probability distribution p(x, t). (a and b) Experimental data for NHE⁺ and NHE⁻ cells, respectively, at different time points t = 1, 120, and 480 min in a semilogarithmic representation. The continuous blue and orange lines show the solutions of the fractional diffusion equation as given in Eq. 9 with the parameter set obtained by the msd fit in Table 1. Analogously, the green lines depict the Gaussian Ornstein–Uhlenbeck functions. For t = 1 min, the probability distribution of the data points shows a peaked structure clearly deviating from a Gaussian form. (c) The kurtosis of the distribution function p(x, t) varies as a function of time and saturates at ≈2.3 for long times. Being different from the value of 3 (green line, OU), the kurtosis confirms the deviation from a Gaussian (Ornstein–Uhlenbeck) probability distribution. The continuous blue and orange lines (FKK) represent the kurtosis modeled with the fractional Klein–Kramers equation including a Gaussian noise term.

Fig. 3.

Decay of the velocity autocorrelation function. The points represent the experimental data for MDCK-F NHE⁺ (a) and NHE⁻ (b) cells. The continuous blue and orange curves display the velocity correlation function of the Klein–Kramers equation (FKK) given by the Mittag-Leffler function in Eq. 7 with the parameters of Table 1. The uncertainties of the fractional Klein–Kramers model estimation are indicated as dashed black lines. The green lines display the exponential decay of the Ornstein–Uhlenbeck process (OU). Whereas the fractional velocity autocorrelation function of the Klein–Kramers equation reliably models the experimental data, the Ornstein–Uhlenbeck process fails to do so.