Changes in the hyperelastic properties of endothelial cells induced by tumor necrosis factor-alpha
- PMID: 18199670
- PMCID: PMC2275697
- DOI: 10.1529/biophysj.106.099333
Changes in the hyperelastic properties of endothelial cells induced by tumor necrosis factor-alpha
Abstract
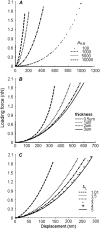
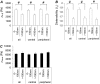
Mechanical properties of living cells can be determined using atomic force microscopy (AFM). In this study, a novel analysis was developed to determine the mechanical properties of adherent monolayers of pulmonary microvascular endothelial cells (ECs) using AFM and finite element modeling, which considers both the finite thickness of ECs and their nonlinear elastic properties, as well as the large strain induced by AFM. Comparison of this model with the more traditional Hertzian model, which assumes linear elastic behavior, small strains, and infinite cell thickness, suggests that the new analysis can predict the mechanical response of ECs during AFM indentation better than Hertz's model, especially when using force-displacement data obtained from large indentations (>100 nm). The shear moduli and distensibility of ECs were greater when using small indentations (<100 nm) compared to large indentations (>100 nm). Tumor necrosis factor-alpha induced changes in the mechanical properties of ECs, which included a decrease in the average shear moduli that occurred in all regions of the ECs and an increase in distensibility in the central regions when measured using small indentations. These changes can be modeled as changes in a chain network structure within the ECs.
Figures







Similar articles
-
Heterogeneous elastic response of human lung microvascular endothelial cells to barrier modulating stimuli.Nanomedicine. 2013 Oct;9(7):875-84. doi: 10.1016/j.nano.2013.03.006. Epub 2013 Mar 20. Nanomedicine. 2013. PMID: 23523769 Free PMC article.
-
Effect of neutrophil adhesion on the mechanical properties of lung microvascular endothelial cells.Am J Respir Cell Mol Biol. 2010 Nov;43(5):591-8. doi: 10.1165/rcmb.2006-0381OC. Epub 2009 Dec 18. Am J Respir Cell Mol Biol. 2010. PMID: 20023207 Free PMC article.
-
Probing mechanical properties of living cells by atomic force microscopy with blunted pyramidal cantilever tips.Phys Rev E Stat Nonlin Soft Matter Phys. 2005 Aug;72(2 Pt 1):021914. doi: 10.1103/PhysRevE.72.021914. Epub 2005 Aug 29. Phys Rev E Stat Nonlin Soft Matter Phys. 2005. PMID: 16196611
-
Mechanosensitive properties in the endothelium and their roles in the regulation of endothelial function.J Cardiovasc Pharmacol. 2013 Jun;61(6):461-70. doi: 10.1097/FJC.0b013e31828c0933. J Cardiovasc Pharmacol. 2013. PMID: 23429585 Review.
-
Mechanotransduction and the glycocalyx.J Intern Med. 2006 Apr;259(4):339-50. doi: 10.1111/j.1365-2796.2006.01620.x. J Intern Med. 2006. PMID: 16594902 Review.
Cited by
-
Heterogeneous elastic response of human lung microvascular endothelial cells to barrier modulating stimuli.Nanomedicine. 2013 Oct;9(7):875-84. doi: 10.1016/j.nano.2013.03.006. Epub 2013 Mar 20. Nanomedicine. 2013. PMID: 23523769 Free PMC article.
-
Poroelastic osmoregulation of living cell volume.iScience. 2021 Nov 22;24(12):103482. doi: 10.1016/j.isci.2021.103482. eCollection 2021 Dec 17. iScience. 2021. PMID: 34927026 Free PMC article.
-
Nanobiomechanics of living cells: a review.Interface Focus. 2014 Apr 6;4(2):20130055. doi: 10.1098/rsfs.2013.0055. Interface Focus. 2014. PMID: 24748952 Free PMC article. Review.
-
Erythrocyte flow through the interendothelial slits of the splenic venous sinus.Biomech Model Mechanobiol. 2021 Dec;20(6):2227-2245. doi: 10.1007/s10237-021-01503-y. Epub 2021 Sep 18. Biomech Model Mechanobiol. 2021. PMID: 34535857 Free PMC article.
-
Determination of the elastic moduli of thin samples and adherent cells using conical atomic force microscope tips.Nat Nanotechnol. 2012 Nov;7(11):733-6. doi: 10.1038/nnano.2012.163. Epub 2012 Sep 30. Nat Nanotechnol. 2012. PMID: 23023646 Free PMC article.
References
-
- Tajaddini, A., D. L. Kilpatrick, and D. G. Vince. 2003. A novel experimental method to estimate stress-strain behavior of intact coronary arteries using intravascular ultrasound (IVUS). J. Biomech. Eng. 125:120–123. - PubMed
-
- Kilpatrick, D., C. Xu, R. Vito, and S. Glagov. 2002. Correlation of mechanical behavior and MMP-1 presence in human atherosclerotic plaque. J. Mech. Med. Biol. 2:1–7.
-
- Samani, A., and D. Plewes. 2004. A method to measure the hyperelastic parameters of ex vivo breast tissue samples. Phys. Med. Biol. 49:4395–4405. - PubMed
-
- Krouskop, T. A., T. M. Wheeler, F. Kallel, B. S. Garra, and T. Hall. 1998. Elastic moduli of breast and prostate tissues under compression. Ultrason. Imaging. 20:260–274. - PubMed
-
- Marchant, R. E., I. Kang, P. S. Sit, Y. Zhou, B. A. Todd, S. J. Eppell, and I. Lee. 2002. Molecular views and measurements of hemostatic processes using atomic force microscopy. Curr. Protein Pept. Sci. 3:249–274. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

