Defining functional distances over gene ontology

Abstract

Background: A fundamental problem when trying to define the functional relationships between proteins is the difficulty in quantifying functional similarities, even when well-structured ontologies exist regarding the activity of proteins (i.e. 'gene ontology' -GO-). However, functional metrics can overcome the problems in the comparing and evaluating functional assignments and predictions. As a reference of proximity, previous approaches to compare GO terms considered linkage in terms of ontology weighted by a probability distribution that balances the non-uniform 'richness' of different parts of the Direct Acyclic Graph. Here, we have followed a different approach to quantify functional similarities between GO terms.

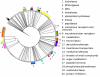
Results: We propose a new method to derive 'functional distances' between GO terms that is based on the simultaneous occurrence of terms in the same set of Interpro entries, instead of relying on the structure of the GO. The coincidence of GO terms reveals natural biological links between the GO functions and defines a distance model Df which fulfils the properties of a Metric Space. The distances obtained in this way can be represented as a hierarchical 'Functional Tree'.

Conclusion: The method proposed provides a new definition of distance that enables the similarity between GO terms to be quantified. Additionally, the 'Functional Tree' defines groups with biological meaning enhancing its utility for protein function comparison and prediction. Finally, this approach could be for function-based protein searches in databases, and for analysing the gene clusters produced by DNA array experiments.

Figure 1

Scheme of the method used for obtaining the Metric Model based on Gene Ontology annotations. (1) Profile vectors are built by retrieving the Molecular Function Gene Ontology annotations (MF-GO terms) of Interpro domains from the file interpro2go. (2) From the profiles, a co-occurrence matrix is calculated by counting how many times two MF-GO terms occur in the same set of Interpro domains. (3) The co-occurrence vectors are feature vectors that describe the functional links of each MF-GO term. The similarity between the MF-GO terms is calculated by the cosine distance between the vectors. (4) The similarity values are arranged in a matrix S. The similarity matrix was considered as the Adjacency Matrix of a weighted graph G. The terms can be clustered by means of the partition of the graph. To obtain the best partition of G, a Spectral Clustering algorithm is applied. The Spectral Clustering algorithm projects the terms in a K dimensional space which can be clustered with standard clustering techniques. (5) The GO terms are grouped in a Hierarchical Tree representing the Functional Distance D_f that satisfy the mathematical properties of a Metric Space.

Figure 2

(A) Initial Similarity matrix of 1329 × 1329 dimensions. The similarity colour scale is shown at the right of the matrix. S is obtained from the set of co-occurrence vectors. Note that S is symmetric, positive, and its values are ranked between 0 and 1. (B) Distribution of the similarity values. The distribution shows that S is sparse and depicts a general view of the structure of the search space for the clustering of S.

Figure 3

Scheme of the spectral clustering methodology. Spectral clustering techniques aim to find the best partition of a weighted graph. A graph is constructed where the nodes are MF-GO terms linked by similarity values s_ij derived by calculating the cosine distance between the vectors of the co-occurrence matrix. The similarity matrix S = [s_ij] is treated as a real-value adjacency matrix of the graph. Let P be a normalized matrix named the Transition Probability matrix that represents the probability of transit from one node to another in this weighted graph. P is calculated from S. The first K eigenvalues of P are used to map the nodes of the graph to a K-dimensional space and the points in this reduced space can be grouped by any clustering algorithm. In this work, we have applied a hierarchical clustering algorithm.

Figure 4

Functional Tree representation. The tree is divided into 93 groups. The groups for which a functional 'homogeneity' was qualitatively assessed are labelled and coloured over the tree. The functional labels are specified. The tree was generated with iTol [30].

Figure 5

Comparison between functional distance and sequence similarity for pairs of Yeast proteins annotated with TAS and IDA evidence codes. The alignments covers most of the range of sequence similarities, whose distribution is shown in panel D. (A) Hausdorff distance (calculated using our functional metric) vs. sequence identity. The mean and the deviation values for each interval are also shown. (B) Hausdorff distance calculated using Lord's Semantic Similarity vs. sequence identity. (C) Mean values for both distance metrics. (D) Distribution of the percentage of Yeast protein pairs in each sequence similarity category.

Figure 6

(A) Similarity Matrix in spectral space. The rows of the matrix represent the MF-GO terms in the reduced space of dimension 93. The terms are stacked in the same order that the Functional Tree (B) Ordered Similarity Matrix. The matrix was packed according to the optimal clustering. Each diagonal block correspond to a group in the Functional Tree. This matrix is close to an ideal block diagonal matrix (correlation coefficient of 0.86) that reveals a compact structure of functional groups.

Figure 7

Graph representation of the ontology relations of a subset of MF-GO terms belonging to 'group 3' of the Functional Tree (orange nodes). The nodes in blue (GO:0016566 and GO:0003700) correspond to members of the 'group 3' that are also annotations of the pair [Uniprot:P20134]/[Uniprot:P10961]. The paths that links them are highlighted in black. Note there are two paths that connect them, and the least common ancestor is the node GO:0030528 ('transcription regulator activity') one level down from the root node. The Semantic Distance of the protein pair [Uniprot:P20134]/[Uniprot:P10961] is 0.76 whereas the Functional Distance is close to 0.

Figure 8

The whole spectra of the P matrix [λ_i(P)]_i∈U is analyzed selecting the first K eigenvalues and for each selection obtaining a partition of the MF-GO terms C_K. In panel A, the values of the gap measure calculated for C_K are represented and according to the Spectral Clustering theory, the best partition C* minimizes the gap value. The red circle encloses the eigenvalues of the spectra that generate 'good' clusterings (interval [4, 93]). Panel B shows the result of applying a second criterion to select the best number of groups from the interval. The correlation coefficient of the ordered similarity matrix with an ideal block diagonal matrix is calculated for each partition. The best clustering is obtained by selecting the first 93 eigenvalues.