Biophysical study of thermal denaturation of apo-calmodulin: dynamics of native and unfolded states

Abstract

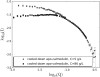
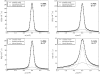
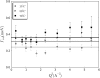
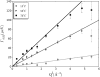
Apo-calmodulin, a small, mainly alpha, soluble protein is a calcium-dependent protein activator. This article presents a study of internal dynamics of native and thermal unfolded apo-calmodulin, using quasi-elastic neutron scattering. This technique can probe protein internal dynamics in the picosecond timescale and in the nanometer length-scale. It appears that a dynamical transition is associated with thermal denaturation of apo-calmodulin. This dynamical transition goes together with a decrease of the confinement of hydrogen atoms, a decrease of immobile protons proportion and an increase of dynamical heterogeneity. The comparison of native and unfolded states dynamics suggests that the dynamics of protein atoms is more influenced by their distance to the backbone than by their solvent exposure.

FIGURE 1

log₁₀(I) versus log₁₀(Q) representation of SANS spectra of apo-calmodulin cooled down to room temperature after heating up to 70°C, at 5 g/L (•) and at 86 g/L (○).

FIGURE 2

Guinier representation of quasi-elastic intensity, S(Q, ω = 0), or, more precisely, of apo-calmodulin at several temperatures: ○, 15°C; 50°C; and □, 70°C. (Solid lines) Linear fits leading to the mean-square displacement 〈u²〉. The calmodulin concentration was 86 g/L.

FIGURE 3

Quasi-elastic spectra of apo-calmodulin at two Q-values, 1 Å⁻¹ and 2 Å⁻¹ and two temperatures, 15°C and 70°C. (Solid lines) The fit of the complete model (Eq. 12). (Dashed lines) Lorentzian describing internal motions (L_int). (Dotted lines) Lorentzian describing translational diffusion (L_diff). The calmodulin concentration was 86 g/L.

FIGURE 4

Width Γ_int of the Lorentzian function describing internal motions, L_int, of apo-calmodulin as a function of Q² at several temperatures: ○, 15°C; 50°C; and □, 70°C. (Solid lines) Fits in the region leading to the diffusion coefficient D_sph (see Eq. 23).

FIGURE 5

Width Γ_diff of the Lorentzian function describing global translational diffusion, L_diff, of apo-calmodulin as a function of Q² at several temperatures: ○, 15°C; 50°C; and □, 70°C. (Solid lines) Linear fits leading to the diffusion coefficient D_t. The resolution of the experiment was 90 μeV (HWHM).

FIGURE 6

Elastic incoherent structure factor (EISF) of apo-calmodulin as a function of Q at several temperatures: ○, 15°C; 50°C; and □, 70°C. (Solid lines) Fits using Eq. 27, leading to the immobile protons proportion p, the mean radius of spheres in which hydrogen atoms diffuse 〈a〉, and the polydispersity index of spheres volumes, The inset shows the lognormal distributions of sphere radii given by the fit of the experimental EISF.

FIGURE 7

Schematic representation of the assumed behavior of the protons populations. (A) Native state. (Blue) Radii of sphere of the different populations. (Black) Fitted model, including a proportion p of immobile protons, and a lognormal distribution of sphere radii. (B) Unfolded state. (Red) Radii of sphere of the different populations. (Dashed blue line) Radii of sphere of the different populations in native state. (Black) Fitted model, including a proportion p of immobile protons, and a log-normal distribution of sphere radii.