Instability-associated changes in contact stress and contact stress rates near a step-off incongruity

Abstract

Background: Intra-articular fractures can result in articular surface incongruity and joint instability, both of which can lead to posttraumatic osteoarthritis. The purpose of this study was to quantify changes in contact stresses and contact stress rates in incongruous human cadaveric ankles that were either stable or unstable. It was hypothesized that joint instability, superimposed on articular incongruity, would cause significant increases in contact stresses and contact stress rates.

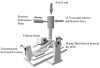
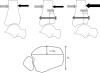
Methods: Intact human cadaveric ankles were subjected to quasi-physiologic stance-phase motion and loading, and instantaneous contact stresses were captured at 132 Hz. The anterior one-third of the distal part of the tibia was displaced proximally by 2.0 mm, and testing was repeated. Anterior/posterior forces were modulated during loading to cause incongruous ankles to either remain stable or become unstable during loading. Transient contact stresses and contact stress rates were measured for seven ankles under intact, stable-incongruous, and unstable-incongruous conditions. Peak and 95th percentile values of contact stress and contact stress rates for all three conditions were compared to determine the pathomechanical effects of incongruity and instability.

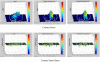
Results: The addition of instability caused 95th percentile and peak contact stresses to increase approximately between 20% and 25% in the unstable-incongruous specimens compared with the stable-incongruous specimens. In contrast, the addition of instability increased the magnitude of peak positive and peak negative contact stress rates by 115% and 170% in the unstable-incongruous specimens compared with the stable-incongruous specimens. Similarly, the 95th percentile contact stress rates increased 112% in the unstable-incongruous specimens compared with the stable-incongruous specimens.

Conclusions: In human cadaveric ankles, instability superimposed on an existing articular surface incongruity causes disproportionate increases in contact stress rates compared with the increases in contact stresses.

Figure 1

The custom testing fixture applied axial load and directed plantardorsi flexion of the ankle via an MTS. The anterior-posterior forces were applied by two separate pneumatic cylinders. The forefoot and heel were rigidly secured with PMMA allowing unconstrained motion of the ankle, midfoot, and hindfoot.

Figure 2

The anterior one-third of the distal tibial articular surface was osteotomized and displaced 2.0 mm proximally and secured with a lag bolt to create potentially unstable incongruous specimens. A 30 N anteriorly directed force (grey arrows) had to be applied to the tibia to prevent spontaneous anterior subluxation of the talus during axial loading. To create subluxation, a posteriorly-directed pulse (black arrows) was increased in magnitude until subluxation occurred. The subluxation pulse varied between 0 N and 120 N in 20 N increments and were randomly applied. The smallest subluxation pulse that caused subluxation (large black arrow) was defined as that specimen’s specific instability-threshold subluxation pulse. The subluxation pulse 20 N less than the instability-threshold pulse (smaller black arrow) was defined as that specimen’s specific metastable-limit subluxation pulse. Intact specimens were subjected to the same anteriorly-directed stabilization forces and posteriorly-directed subluxation pulses.

Figure 3

Ankles coursed through physiologic motion of the gait cycle. During the heel-off phase of the gait cycle, the posteriorly-directed subluxation pulse was ramped linearly from 0 N to its specified magnitude and back down to 0 N (representing the 45% to 70% phase of the gait cycle).

Figure 4

Tibiotalar sagittal displacement in intact conditions demonstrated a linear relationship over the entire range of subluxation pulses. Intact specimens were never observed to subluxate. In incongruous conditions, specimens remained stable until the subluxation pulse exceeded a critical limit (instability-threshold) and rapid increases in tibiotalar displacement were measured. In the specimen depicted in the figure, the metastable-limit pulse is 60 N and the instability-threshold pulse is 80 N.

Figure 5

Peak and 95^th percentile contact stresses and contact stress rates are shown as a percentage of corresponding intact condition values. Both peak and 95^th percentile contact stresses in the unstable-incongruous condition were only modestly elevated compared to the stable-incongruous condition. In contrast, instability-associated changes in peak and 95^th percentile contact stress rates in the unstable-incongruous condition were substantially elevated compared to the stable-incongruous condition. The data clearly demonstrate that instability had a substantially greater effect on contact stress rates compared to contact stresses in incongruous specimens.

Figure 6

Contact stress and contact stress rate contour plots demonstrate feature differences between intact, stable-incongruous, and unstable-incongruous condtions. Fig. 6a: Just prior to application of the subluxation pulse, contact stresses and contact stress rates are homogenous in all three conditions. The osteotomy border is clearly delineated in incongruous conditions. Fig. 6b: At the onset of subluxation in the unstable-incongruous condition, contact stresses have shifted anteriorly in all conditions with contact stress concentration aligned at the ostetomy border in the incongruous conditions. In the intact and stable-incongruous conditions, contact stress rates are low-magnitude and homogenous. In the unstable-incongruous condition, a sharp focus of negative contact stress rate along the posterior border of the osteotomy is evident (black arrow). Fig 6c: At the point of maximum subluxation, the focus of contact stress on the anterior fragment is evident in the unstable-incongruous condition. However, contact stress magnitudes are similar between all three conditions. Contact stress rates remain uniformly low and homogenous in the intact and stable-incongruous conditions. In contrast, a sharp focus of positive contact stress rate is obvious on the anterior fragment with a corresponding focus of negative contact stress rate on the posterior border of the osteotomy in the unstable-incongruous condition. Fig 6d. After the subluxation pulse had returned to 0 N, and the unstable-incongruous condition had reduced, contact stresses and contact stress rates had returned to previous homogenous low-level values in all conditions.

Figure 6

Contact stress and contact stress rate contour plots demonstrate feature differences between intact, stable-incongruous, and unstable-incongruous condtions. Fig. 6a: Just prior to application of the subluxation pulse, contact stresses and contact stress rates are homogenous in all three conditions. The osteotomy border is clearly delineated in incongruous conditions. Fig. 6b: At the onset of subluxation in the unstable-incongruous condition, contact stresses have shifted anteriorly in all conditions with contact stress concentration aligned at the ostetomy border in the incongruous conditions. In the intact and stable-incongruous conditions, contact stress rates are low-magnitude and homogenous. In the unstable-incongruous condition, a sharp focus of negative contact stress rate along the posterior border of the osteotomy is evident (black arrow). Fig 6c: At the point of maximum subluxation, the focus of contact stress on the anterior fragment is evident in the unstable-incongruous condition. However, contact stress magnitudes are similar between all three conditions. Contact stress rates remain uniformly low and homogenous in the intact and stable-incongruous conditions. In contrast, a sharp focus of positive contact stress rate is obvious on the anterior fragment with a corresponding focus of negative contact stress rate on the posterior border of the osteotomy in the unstable-incongruous condition. Fig 6d. After the subluxation pulse had returned to 0 N, and the unstable-incongruous condition had reduced, contact stresses and contact stress rates had returned to previous homogenous low-level values in all conditions.

Figure 6

Contact stress and contact stress rate contour plots demonstrate feature differences between intact, stable-incongruous, and unstable-incongruous condtions. Fig. 6a: Just prior to application of the subluxation pulse, contact stresses and contact stress rates are homogenous in all three conditions. The osteotomy border is clearly delineated in incongruous conditions. Fig. 6b: At the onset of subluxation in the unstable-incongruous condition, contact stresses have shifted anteriorly in all conditions with contact stress concentration aligned at the ostetomy border in the incongruous conditions. In the intact and stable-incongruous conditions, contact stress rates are low-magnitude and homogenous. In the unstable-incongruous condition, a sharp focus of negative contact stress rate along the posterior border of the osteotomy is evident (black arrow). Fig 6c: At the point of maximum subluxation, the focus of contact stress on the anterior fragment is evident in the unstable-incongruous condition. However, contact stress magnitudes are similar between all three conditions. Contact stress rates remain uniformly low and homogenous in the intact and stable-incongruous conditions. In contrast, a sharp focus of positive contact stress rate is obvious on the anterior fragment with a corresponding focus of negative contact stress rate on the posterior border of the osteotomy in the unstable-incongruous condition. Fig 6d. After the subluxation pulse had returned to 0 N, and the unstable-incongruous condition had reduced, contact stresses and contact stress rates had returned to previous homogenous low-level values in all conditions.

Figure 6

Contact stress and contact stress rate contour plots demonstrate feature differences between intact, stable-incongruous, and unstable-incongruous condtions. Fig. 6a: Just prior to application of the subluxation pulse, contact stresses and contact stress rates are homogenous in all three conditions. The osteotomy border is clearly delineated in incongruous conditions. Fig. 6b: At the onset of subluxation in the unstable-incongruous condition, contact stresses have shifted anteriorly in all conditions with contact stress concentration aligned at the ostetomy border in the incongruous conditions. In the intact and stable-incongruous conditions, contact stress rates are low-magnitude and homogenous. In the unstable-incongruous condition, a sharp focus of negative contact stress rate along the posterior border of the osteotomy is evident (black arrow). Fig 6c: At the point of maximum subluxation, the focus of contact stress on the anterior fragment is evident in the unstable-incongruous condition. However, contact stress magnitudes are similar between all three conditions. Contact stress rates remain uniformly low and homogenous in the intact and stable-incongruous conditions. In contrast, a sharp focus of positive contact stress rate is obvious on the anterior fragment with a corresponding focus of negative contact stress rate on the posterior border of the osteotomy in the unstable-incongruous condition. Fig 6d. After the subluxation pulse had returned to 0 N, and the unstable-incongruous condition had reduced, contact stresses and contact stress rates had returned to previous homogenous low-level values in all conditions.

Figure 7

Representative contact stress and contact stress rate contour plots during the subluxation event in the unstable-incongruous condition. Fig. 7a. Four consecutive contour plots demonstrate how the talus perches on the posterior border of the osteotomy and subsequently subluxates anteriorly over 0.023 seconds contacting the anterior fragment. Fig 7b. Four consecutive contour plots of contact stress rates clearly depict the subluxation event. As the talus subluxates anteriorly, it appears to rapidly unload the posterior border of the osteotomy. High negative contact stress rates are measured along this border. As the talus abruptly contacts the anterior osteotomized fragment, a rapid rise in positive contact stress rate occurs on this fragment.

Figure 7

Representative contact stress and contact stress rate contour plots during the subluxation event in the unstable-incongruous condition. Fig. 7a. Four consecutive contour plots demonstrate how the talus perches on the posterior border of the osteotomy and subsequently subluxates anteriorly over 0.023 seconds contacting the anterior fragment. Fig 7b. Four consecutive contour plots of contact stress rates clearly depict the subluxation event. As the talus subluxates anteriorly, it appears to rapidly unload the posterior border of the osteotomy. High negative contact stress rates are measured along this border. As the talus abruptly contacts the anterior osteotomized fragment, a rapid rise in positive contact stress rate occurs on this fragment.