Optimal foraging: Lévy pattern or process?
- PMID: 18292078
- PMCID: PMC2607432
- DOI: 10.1098/rsif.2008.0006
Optimal foraging: Lévy pattern or process?
Abstract
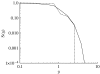
Many different species have been suggested to forage according to a Lévy walk in which the distribution of step lengths is heavy-tailed. Theoretical research has shown that a Lévy exponent of approximately 2 can provide a higher foraging efficiency than other exponents. In this paper, a composite search model is presented for non-destructive foraging behaviour based on Brownian (i.e. non-heavy-tailed) motion. The model consists of an intensive search phase, followed by an extensive phase, if no food is found in the intensive phase. Quantities commonly observed in the field, such as the distance travelled before finding food and the net displacement in a fixed time interval, are examined and compared with the results of a Lévy walk model. It is shown that it may be very difficult, in practice, to distinguish between the Brownian and the Lévy models on the basis of observed data. A mathematical expression for the optimal time to switch from intensive to extensive search mode is derived, and it is shown that the composite search model provides higher foraging efficiency than the Lévy model.
Figures
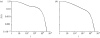
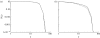

Similar articles
-
The Lévy flight foraging hypothesis in a pelagic seabird.J Anim Ecol. 2014 Mar;83(2):353-64. doi: 10.1111/1365-2656.12147. Epub 2013 Nov 4. J Anim Ecol. 2014. PMID: 24102157
-
Optimal foraging strategies for mutually avoiding competitors.J Theor Biol. 2023 Aug 7;570:111537. doi: 10.1016/j.jtbi.2023.111537. Epub 2023 May 18. J Theor Biol. 2023. PMID: 37207720
-
Optimal Lévy-flight foraging in a finite landscape.J R Soc Interface. 2015 Mar 6;12(104):20141158. doi: 10.1098/rsif.2014.1158. J R Soc Interface. 2015. PMID: 25631566 Free PMC article.
-
Liberating Lévy walk research from the shackles of optimal foraging.Phys Life Rev. 2015 Sep;14:59-83. doi: 10.1016/j.plrev.2015.03.002. Epub 2015 Mar 20. Phys Life Rev. 2015. PMID: 25835600 Review.
-
Assessing Lévy walks as models of animal foraging.J R Soc Interface. 2011 Sep 7;8(62):1233-47. doi: 10.1098/rsif.2011.0200. Epub 2011 Jun 1. J R Soc Interface. 2011. PMID: 21632609 Free PMC article. Review.
Cited by
-
Random walk models in biology.J R Soc Interface. 2008 Aug 6;5(25):813-34. doi: 10.1098/rsif.2008.0014. J R Soc Interface. 2008. PMID: 18426776 Free PMC article. Review.
-
Patterns of interaction-dominant dynamics in individual versus collaborative memory foraging.Cogn Process. 2015 Nov;16(4):389-99. doi: 10.1007/s10339-015-0731-8. Epub 2015 Aug 28. Cogn Process. 2015. PMID: 26314586
-
Search strategies of ants in landmark-rich habitats.J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2008 Nov;194(11):929-38. doi: 10.1007/s00359-008-0365-8. Epub 2008 Sep 10. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2008. PMID: 18781312
-
The evolutionary origins of Lévy walk foraging.PLoS Comput Biol. 2017 Oct 3;13(10):e1005774. doi: 10.1371/journal.pcbi.1005774. eCollection 2017 Oct. PLoS Comput Biol. 2017. PMID: 28972973 Free PMC article.
-
Multiscale Computation and Dynamic Attention in Biological and Artificial Intelligence.Brain Sci. 2020 Jun 20;10(6):396. doi: 10.3390/brainsci10060396. Brain Sci. 2020. PMID: 32575758 Free PMC article. Review.
References
-
- Austin D, Bowen W.D, McMillan J.I. Intraspecific variation in movement patterns: modeling individual behaviour in a large marine predator. Oikos. 2004;105:15–30. doi: 10.1111/j.0030-1299.1999.12730.x. - DOI
MeSH terms
LinkOut - more resources
Full Text Sources

