Effects of dependence in high-dimensional multiple testing problems

Abstract

Background: We consider effects of dependence among variables of high-dimensional data in multiple hypothesis testing problems, in particular the False Discovery Rate (FDR) control procedures. Recent simulation studies consider only simple correlation structures among variables, which is hardly inspired by real data features. Our aim is to systematically study effects of several network features like sparsity and correlation strength by imposing dependence structures among variables using random correlation matrices.

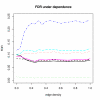
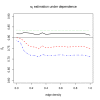
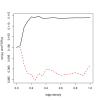
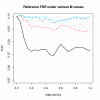
Results: We study the robustness against dependence of several FDR procedures that are popular in microarray studies, such as Benjamin-Hochberg FDR, Storey's q-value, SAM and resampling based FDR procedures. False Non-discovery Rates and estimates of the number of null hypotheses are computed from those methods and compared. Our simulation study shows that methods such as SAM and the q-value do not adequately control the FDR to the level claimed under dependence conditions. On the other hand, the adaptive Benjamini-Hochberg procedure seems to be most robust while remaining conservative. Finally, the estimates of the number of true null hypotheses under various dependence conditions are variable.

Conclusion: We discuss a new method for efficient guided simulation of dependent data, which satisfy imposed network constraints as conditional independence structures. Our simulation set-up allows for a structural study of the effect of dependencies on multiple testing criterions and is useful for testing a potentially new method on pi0 or FDR estimation in a dependency context.

Figure 1

Average FDR results under dependence when π₀ = 0.8. The x-axis corresponds to the proportion of edges in the network and the y-axis corresponds to FDR estimates for various procedures. Testing cut-off c is tuned such that true FDR is 0.1 under independence. FDR(c) (solid black) represents true FDR values in terms of (5) using the fixed c. The FDR procedures and corresponding lines in this figure are the following ones: BH (dashed red), BY (dotted green), SAM (dot-dashed blue), Qvalue (dashed cyan), ABH (purple), the upper limit RBH (dashed black), the point RBH (dotted red).

Figure 2

Average FDR results under dependence when π₀ = 0.95. See Figure 1 for explanation.

Figure 3

Average FNR results under dependence when π₀ = 0.8. The y-axis corresponds to FNR estimates for various procedures. For the other explanation, see Figure 1.

Figure 4

Average π₀ estimates under dependence when π₀ = 0.8. The x-axis corresponds to the proportion of edges in the network and the y-axis corresponds to π₀ estimates for various procedures. The π₀ estimators and corresponding lines are SAM (solid black), Qvalue (dashed red), ABH (dotted green) and the convex estimator of Langaas et al [10] (dot-dashed).

Figure 5

Variances of correlations and FDR(c) when π₀ = 0.8. The solid line represents variance of correlations and the dashed line represents FDR(c). For comparison, we transform var(ρ_ij) to var(ρ_ij)/10 + 0.1 so that two quantities have same scale.

Figure 6

FDR(c) with different M values. For various M - m values, FDR(c) is computed. The M - m values and corresponding lines are 1001 (solid black), 1010 (dashed red), 1025 (dotted green), 1046 (dot-dashed blue) and 1073 (dashed cyan).

Figure 7

Graphical representation of conditional independence structures when m = 4. A sequence of possible nested structure is depicted when the number of nodes is 4. The left most graph represents complete independence between variables and the right most graph represents complete dependence between variables. The dependence structure of every left graph is contained to the structure of the graph right to it.