Boolean network model predicts cell cycle sequence of fission yeast
- PMID: 18301750
- PMCID: PMC2243020
- DOI: 10.1371/journal.pone.0001672
Boolean network model predicts cell cycle sequence of fission yeast
Abstract
A Boolean network model of the cell-cycle regulatory network of fission yeast (Schizosaccharomyces Pombe) is constructed solely on the basis of the known biochemical interaction topology. Simulating the model in the computer faithfully reproduces the known activity sequence of regulatory proteins along the cell cycle of the living cell. Contrary to existing differential equation models, no parameters enter the model except the structure of the regulatory circuitry. The dynamical properties of the model indicate that the biological dynamical sequence is robustly implemented in the regulatory network, with the biological stationary state G1 corresponding to the dominant attractor in state space, and with the biological regulatory sequence being a strongly attractive trajectory. Comparing the fission yeast cell-cycle model to a similar model of the corresponding network in S. cerevisiae, a remarkable difference in circuitry, as well as dynamics is observed. While the latter operates in a strongly damped mode, driven by external excitation, the S. pombe network represents an auto-excited system with external damping.
Conflict of interest statement
Figures
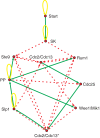
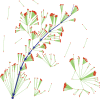
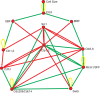
References
-
- Gunsalus KC, Ge H, Schetter AJ, Goldberg DS, Han J-DJ, et al. Predictive models of molecular machines involved in Caenorhabditis elegans early embryogenesis. Nature. 2005;436 (11):861–865. - PubMed
-
- Hasty J, McMillen D, Isaacs F, Collins JJ. Computational studies of gene regulatory networks: in numero molecular biology. Nat Rev Genet. 2001;2:268–279. - PubMed
-
- Riel NAW. Dynamic modelling and analysis of biochemical networks: mechanism-based models and model-based experiments. Briefings in Bioinformatics. 2006;7(4):364–374. - PubMed
-
- Smolen P, Baxter DA, Byrne JH. Mathematical modeling of gene networks. Neuron. 2000;26:567–580. - PubMed
-
- Gillespie DT. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions, J Comp Phys. 1976;22:403–434.
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

