Robust score statistics for QTL linkage analysis

Abstract

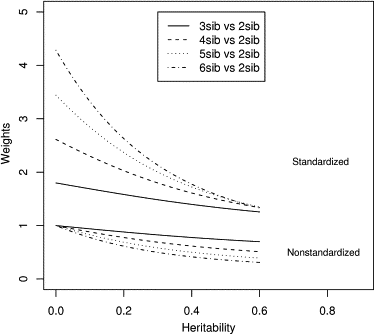
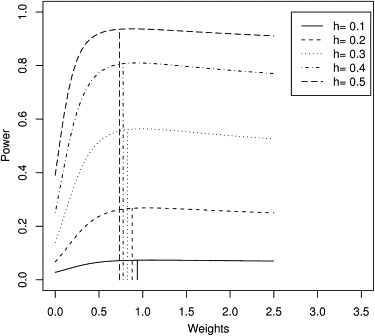
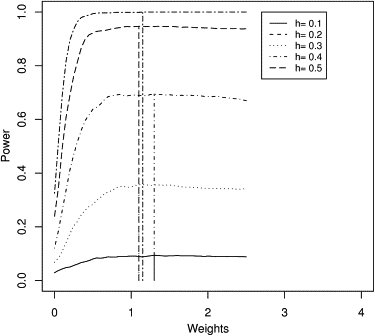
The traditional variance components approach for quantitative trait locus (QTL) linkage analysis is sensitive to violations of normality and fails for selected sampling schemes. Recently, a number of new methods have been developed for QTL mapping in humans. Most of the new methods are based on score statistics or regression-based statistics and are expected to be relatively robust to non-normality of the trait distribution and also to selected sampling, at least in terms of type I error. Whereas the theoretical development of these statistics is more or less complete, some practical issues concerning their implementation still need to be addressed. Here we study some of these issues such as the choice of denominator variance estimates, weighting of pedigrees, effect of parameter misspecification, effect of non-normality of the trait distribution, and effect of incorporating dominance. We present a comprehensive discussion of the theoretical properties of various denominator variance estimates and of the weighting issue and then perform simulation studies for nuclear families to compare the methods in terms of power and robustness. Based on our analytical and simulation results, we provide general guidelines regarding the choice of appropriate QTL mapping statistics in practical situations.

Figure 1

Sensitivity Analysis Results for Mean, Variance, and Correlation Black line gives power for true parameter values. Solid and dashed lines are for over- and underspecification of parameters, respectively. Line colors red, yellow, and blue stand for misspecified mean, variance, and correlation, respectively. Note that the black line roughly coincides with yellow line in almost all cases.

Figure 2

Sensitivity Analysis Results for Skewness and Kurtosis Black line gives power for true parameter values. Solid and dashed lines are for over- and underspecification of parameters, respectively. Line colors cyan and magenta stand for misspecified skewness and kurtosis, respectively. Note that the black line coincides with the cyan and magenta lines for lower-moment statistics.

Figure 3

Analytical Optimal Weights for Sibships Plot of asymptotic optimal weights (analytical) for sibships of sizes 3, 4, 5, and 6 (with respect to a sibship of size 2) as a function of heritability. The lower cluster of plots shows the optimal weights for nonstandardized scores and the upper shows those for standardized scores.

Figure 4

Analytical Power Curves of SCORE.NAÏVE for 3 Sibs Approximate analytical power curves for a population sample with 100 sibships of size 3 and 100 sibpairs. Power is plotted as a function of nonstandardized weight of 3 sibs with respect to 2 sibs. Curves are shown for five different values of heritability (h²). The vertical lines show asymptotic optimal weights for each value of h².

Figure 5

Empirical Power Curves of SCORE.CT for EDAC Pairs Plot of simulation-based power for a combined sample of 20 discordant pairs and 30 concordant pairs. Power is plotted as a function of nonstandardized weight of discordant with respect to concordant pairs. Curves are shown for five different values of heritability (h²). The vertical lines show the actual optimal weights based on simulation, for each value of h².