Calcium-dependent inactivation terminates calcium release in skeletal muscle of amphibians

Abstract

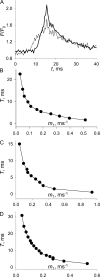
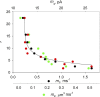
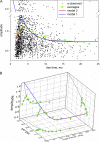
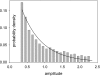
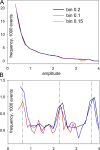
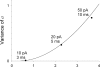
In skeletal muscle of amphibians, the cell-wide cytosolic release of calcium that enables contraction in response to an action potential appears to be built of Ca2+ sparks. The mechanism that rapidly terminates this release was investigated by studying the termination of Ca2+ release underlying sparks. In groups of thousands of sparks occurring spontaneously in membrane-permeabilized frog muscle cells a complex relationship was found between amplitude a and rise time T, which in sparks corresponds to the active time of the underlying Ca2+ release. This relationship included a range of T where a paradoxically decreased with increasing T. Three different methods were used to estimate Ca2+ release flux in groups of sparks of different T. Using every method, it was found that T and flux were inversely correlated, roughly inversely proportional. A simple model in which release sources were inactivated by cytosolic Ca2+ was able to explain the relationship. The predictive value of the model, evaluated by analyzing the variance of spark amplitude, was found to be high when allowance was made for the out-of-focus error contribution to the total variance. This contribution was estimated using a theory of confocal scanning (Ríos, E., N. Shirokova, W.G. Kirsch, G. Pizarro, M.D. Stern, H. Cheng, and A. González. Biophys. J. 2001. 80:169-183), which was confirmed in the present work by simulated line scanning of simulated sparks. Considering these results and other available evidence it is concluded that Ca2+-dependent inactivation, or CDI, provides the crucial mechanism for termination of sparks and cell-wide Ca2+ release in amphibians. Given the similarities in kinetics of release termination observed in cell-averaged records of amphibian and mammalian muscle, and in spite of differences in activation mechanisms, CDI is likely to play a central role in mammals as well. Trivially, an inverse proportionality between release flux and duration, in sparks or in global release of skeletal muscle, maintains constancy of the amount of released Ca2+.

Figure 1.

The relationship between spark rise time and amplitude. (A) Rise time, T, vs. amplitude, a, of 1,887 sparks collected in 700 images of seven frog fibers with permeabilized membrane, placed in standard glutamate solution. Fibers were imaged at 0.135 μm per pixel and 2 ms per line. Sparks were detected and parameters were measured automatically on an interpolated average of three central pixels. Correlation coefficient r ² = 0.015, regression coefficient b = −0.017 ms⁻¹. Inset: top, schematic of the profile F/F ₀ vs. t at the spatial center of the spark, indicating a and T; bottom, Ca²⁺ flux during spark is thought to be roughly constant and last for the rise time. (B) Average a vs. average T in “bins” of increasing T for the group of sparks in A. Bars represent ± SEM of a and T. (C) Average a vs. average T, determined as described for B, for a set of 881 sparks detected in 500 images of two frog fibers imaged at 0.14 μm per pixel and 0.5 ms per line. (D) Average a vs. T, for a set of 6,300 sparks in 1,000 images of four permeabilized fibers placed in sulfate-based solution and imaged at 0.23 μm per pixel and 1.875 ms per line.

Figure 2.

The relationship between rise time and a simple estimator of Ca²⁺ release flux in sparks. (A) Examples of spark profiles used to estimate release flux. Thick trace, F/F ₀ vs. t at the center of the average of the 88 sparks with T between 4 and 5 ms in the group represented in Fig. 1 C. Thin trace, F/F ₀ vs. t for the average of the 18 sparks with T between 9 and 11 ms in the same group. Release flux was estimated by the average rate of rise of normalized fluorescence, m ₁, calculated on bin averages as the ratio a/T, which for the averages shown is respectively 0.234 and 0.069 ms⁻¹. Note that the time-varying rate of rise of fluorescence may diverge substantially from m ₁. (B–D) Bin averages of T plotted against m ₁ for the sets of sparks in Fig. 1, B–D. A similar, strictly monotonic dependence is obtained in all cases.

Figure 3.

Ca²⁺ release flux calculated ab initio. (A) Average of fluorescence in all sparks with T between 4 and 5 ms in the group represented in Fig. 1 A. (B) Release flux density calculated from the average in A, by the “backward” algorithm (details in Materials and methods). The inset is an x-y projection that shows well the narrow footprint of the calculated flux.

Figure 4.

Rise time vs. different estimators of release flux. Black symbols, T vs. m ₁, calculated from binned averages in Fig. 1 B by Eq. 1 (same values as in graph in Fig. 2 B). Green, T vs. m ₂, calculated according to Eq. 2 for the same spark averages. Red, T vs. m ₃, release current calculated by volume integration of flux density derived for the same spark averages by the backward method. Continuous curve, best fit to T vs. m ₃ by Eq. 6. Best fit parameters: k _i β, 2.3 mM⁻¹; k _r, 0.061 ms⁻¹; A* = 0.115.

Figure 5.

Amplitudes and rise times of simulated sparks. Dots plot detected amplitude, a _s vs. rise time in the line scan, T, for sparks generated at random locations in the simulation volume, using a current of 30 pA and release durations Ξ between 0.5 and 35 ms. The sparks represented had a _s > 0.3. Green circles, average values (±SEM) in bins of T containing 300 sparks each. Line, single exponential fit to bin averages (Eq. 7, with b = 0.9409 and k = 0.7337 ms⁻¹). Note that for sparks of constant release flux amplitude increases with T in a saturating manner. Pink symbols, bin averages of a _s for a set of 8,000 sparks simulated with current of 30 pA and Ξ = 5 ms. Note that while Ξ is constant, T varies in a narrow range, being in most cases greater than Ξ. Orange circles, bin averages of a _s of a set of 4,667 sparks simulated assuming the inverse relationship between Ξ and m ₃. (Ξ was exponentially distributed, with a minimum of 0.5 ms. m ₃ was calculated from Ξ by an approximate solution of Eq. 6 and Ξ ∼ T). Note that the dependence between averaged amplitude and T reflects well the inverse relationship between flux and release time assumed in the simulation.

Figure 6.

Model prediction of spark amplitudes. A, dots represent a vs. T for the first set of experimental sparks (as in Fig. 1 A). Circles represent their bin averages (as in Fig. 1 B). The curve in blue plots a as a function of T, calculated with “model 1,” that is, Eqs. 9 and 6, with parameter values given in the legends of Figs. 4 and 5. The curve in red is by “model 2,” for which m ₃ is assumed constant (37 pA) at T < 4.4 ms. Note that in this range of T the a(T) dependence is exponential, given by Eq. 7 scaled by 37/30. (B) Bin-averaged experimental a (circles), prediction by models 1 (blue line) and 2 (red), plotted as a function of both T (as in A) and m ₃. The plot illustrates the model calculation of a, which relies on the bijective correspondence between T and m ₃ given by Eq. 6.

Figure A1.

A fundamental property of measured spark amplitudes. Histogram f(a _s) of scanned amplitudes, a _s, for 10,720 sparks simulated with 30 pA current and 5 ms release duration, placed at random y and z distances from the scanning line. Line plots best fit by the inverse function (Eq. 10). Similar deviations between f and fit were observed in simulations with other parameter values.

Figure A2.

Recovery of “true amplitudes” from distributions of scanned amplitudes. (A) Histograms f(a _s) of scanned amplitudes for a set of sparks consisting in three groups with equal numbers, simulated using three values of current (5, 20, and 50 pA) at three durations (5, 10, and 20 ms). Three alternative binning intervals were used, as indicated. The distribution of true amplitudes in the simulation consists therefore of three Dirac deltas (see below). (B) Distributions g(a) of true amplitudes, derived from f(a _s) in A using Eq. A1. Dashed lines mark the position of true (in-focus) amplitudes of simulated sparks, 0.634, 2.27, and 3.66. Narrow binning is best at locating low amplitude modes and vice versa.

Figure A3.

The amplitude variance due to off-focus spread of spark locations. Circles plot variance of scanned amplitude vs. in-focus amplitude for the three groups of simulated sparks represented in Fig. A2. The curve plots variance vs. true amplitude α, calculated by Eq. 12.