Detailed enzyme kinetics in terms of biochemical species: study of citrate synthase
- PMID: 18350161
- PMCID: PMC2266798
- DOI: 10.1371/journal.pone.0001825
Detailed enzyme kinetics in terms of biochemical species: study of citrate synthase
Abstract
The compulsory-ordered ternary catalytic mechanism for two-substrate two-product enzymes is analyzed to account for binding of inhibitors to each of the four enzyme states and to maintain the relationship between the kinetic constants and the reaction equilibrium constant. The developed quasi-steady flux expression is applied to the analysis of data from citrate synthase to determine and parameterize a kinetic scheme in terms of biochemical species, in which the effects of pH, ionic strength, and cation binding to biochemical species are explicitly accounted for in the analysis of the data. This analysis provides a mechanistic model that is consistent with the data that have been used support competing hypotheses regarding the catalytic mechanism of this enzyme.
Conflict of interest statement
Figures

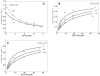
 , with a = [A], b = [B], p = [P], and q = [Q] is illustrated. The four states refer to unbound enzyme (state 1), enzyme-substrate A complex (E·A, state 2), enzyme-substrate A-substrate B complex (E·AB, state 3), and enzyme-product Q complex (E·Q, state 4). The four steps of the catalytic cycle are detailed in Equation (1).
, with a = [A], b = [B], p = [P], and q = [Q] is illustrated. The four states refer to unbound enzyme (state 1), enzyme-substrate A complex (E·A, state 2), enzyme-substrate A-substrate B complex (E·AB, state 3), and enzyme-product Q complex (E·Q, state 4). The four steps of the catalytic cycle are detailed in Equation (1).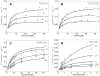


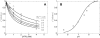

References
-
- Alberty RA. Relations between biochemical thermodynamics and biochemical kinetics. Biophys Chem. 2006;124:11–17. - PubMed
-
- Teusink B, Passarge J, Reijenga CA, Esgalhado E, van der Weijden CC, et al. Can yeast glycolysis be understood in terms of in vitro kinetics of the constituent enzymes? Testing biochemistry. Eur J Biochem. 2000;267:5313–5329. - PubMed
-
- Lambeth MJ, Kushmerick MJ. A computational model for glycogenolysis in skeletal muscle. Ann Biomed Eng. 2002;30:808–827. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

