Directly transmitted viral diseases: modeling the dynamics of transmission

Abstract

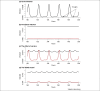
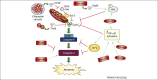
A key hurdle in understanding the spread and control of infectious diseases is to capture appropriately the dynamics of pathogen transmission. As people and goods travel increasingly rapidly around the world, so do pathogens; we must be prepared to understand their spread, in terms of the contact network between hosts, viral life history and within-host dynamics. This will require collaborative work that takes into account viral life history, strategy and evolution, and host genetics, demographics and immunodynamics. Mathematical models are a useful tool for integrating the data and analyses from diverse fields that contribute to our understanding of viral transmission dynamics in heterogeneous host populations.

Figure 1

Model simulations of ten years of epidemic with a variety of parameters. Each graph plots the output of a simulated epidemic over ten years. A transient period of 190 years, not plotted here, was run to move the dynamics onto a stable limit cycle. The proportion of the population infected is plotted as a function of time in years. All simulations were run according to variants of the SEIR (susceptible, exposed, infectious, and recovered) model (Box 1). The model was seasonally forced using a sinusoidal function with a period of one year for more realistic dynamics by varying the transmission coefficient according to β(t). Seasonal forcing is a common phenomenon in childhood infections for which the dynamics are dependent on annual school term cycles. The transmission coefficient, β0, and the infectious period, γ⁻¹, were adjusted for each model to maintain approximately constant R₀, as calculated assuming the sinusoidal term in β(t) = 0. The parameters, unless otherwise specified were: N = 1, γ = 73, σ = 45.625, μ = 1/45, β0 = 1250, β1 = 0.1, ρ = 1. See Table 1 for units and biological interpretations of the parameters. (a) A standard SEIR model for an acute infection with seasonal forcing. The acute, SEIR epidemic model is shown in red in (b), (c) and (d) to highlight the differences. (b) A standard chronic infection with γ = 1, β0 = 17.12329. (c) The carrier model divides the infected class into two groups, those who carry and those who clear the infection. This graph shows the effect of having 1% of the population as carriers, maintaining the infection chronically with β0 = 150.7841 and γ2 = 0.1 or an infectious period of ten years. This has two noticeable effects on the epidemic curve. First, the number of infected individuals at any time is increased. Second, the depth of the troughs (difference between the maximum and minimum number of infected individuals) is smaller in the model with carriers than a homogeneously acute infection (trough depth 0.000202 and 0.00119, respectively). The minimum population size to maintain the expected number of infecteds > 1 is 1004 with carriers, versus 22 975 for the homogeneous acute system. (d) The SEIRS model incorporates a loss of immunity and return to the susceptible class. Loss of immunity in an acute infection results in no longer having biannual cycles, just seasonally forced yearly fluctuations and an overall increase in disease prevalence compared with the acute infection model.

Figure 2

Flow diagrams of viral transmission mathematical models. Each parameter, shown as a Greek letter next to an arrow, defines the rate of movement from one class to the next. μ, birth and death rates; β, transmission coefficient; σ, rate at which infected individuals become infectious; γ, rate at which infectious individuals lose their ability to transmit; ρ, rate of loss of immunity. (a) A schematic of the SEIR model for acute (see Figure 1a) and chronic infections (see Figure 1b) in a homogeneous population with no loss of immunity. (b) The carrier model with a variable infectious period (see Figure 1c). One percent of the population leaves the infectious class at rate γ2, and the other 99% leave at rate γ1. (c) A diagram of the SEIRS model (see Figure 1d). The long arrow from the recovered class to the susceptible class indicates individuals who have recovered from an infection and lose their acquired immunity at rate ρ.