Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2008 Dec;64(4):1009-17.
doi: 10.1111/j.1541-0420.2008.01001.x. Epub 2008 Mar 27.

Inference for constrained estimation of tumor size distributions

Debashis Ghosh  1 , Moulinath Banerjee, Pinaki Biswas
Affiliations

Inference for constrained estimation of tumor size distributions

Debashis Ghosh et al. Biometrics. 2008 Dec.

Abstract

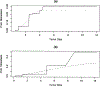
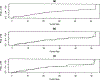
In order to develop better treatment and screening programs for cancer prevention programs, it is important to be able to understand the natural history of the disease and what factors affect its progression. We focus on a particular framework first outlined by Kimmel and Flehinger (1991, Biometrics, 47, 987-1004) and in particular one of their limiting scenarios for analysis. Using an equivalence with a binary regression model, we characterize the nonparametric maximum likelihood estimation procedure for estimation of the tumor size distribution function and give associated asymptotic results. Extensions to semiparametric models and missing data are also described. Application to data from two cancer studies is used to illustrate the finite-sample behavior of the procedure.

PubMed Disclaimer

Figures

Figure 1.
Figure 1.
Estimated fits from model (1) for (A) adenocarcinomas and (B) epidermoids. Solid line on each plot represents NPMLE fit, whereas dashed line represents monotone smoothing spline fit using the method of Ramsay (1998).
Figure 2.
Figure 2.
Distribution function for tumor size at nodal transition for breast cancer SEER data. Figure 2a displays the estimated distribution function for the entire population. Figure 2b shows estimated distribution function stratified by ER status (solid line represents ER-positive cancers, dashed line represents ER-negative cancer). Figure 2c shows estimated distribution function stratified by PR status (solid line represents PR-positive cancers, dashed line represents PR-negative cancers).
See this image and copyright information in PMC

References

    1. Amersi F and Hansen NM (2006). The benefits and limitations of sentinel lymph node biopsy. Current Treatments and Options in Oncology 7, 141–151. - PubMed
    1. Ayer M, Brunk HD, Ewing GM, Reid WT, and Silverman E (1955). An empirical distribution function for sampling with incomplete information. Annals of Mathematical Statistics 26, 641–647.
    1. Banerjee M and Wellner JA (2001). Likelihood ratio tests for monotone functions. Annals of Statistics 29, 1699–1731.
    1. Delgado MA, Rodriguez-Poo JM, and Wolf M (2001). Subsampling inference in cube root asymptotics with an application to Manski’s maximum score estimator. Economics Letters 73, 241–250.
    1. Ghosh D (2006). Modelling tumor biology-progression relationships in screening trials. Statistics in Medicine 25, 1872–1884. - PubMed

Publication types