Optimal enumeration of state space of finitely buffered stochastic molecular networks and exact computation of steady state landscape probability

Abstract

Background: Stochasticity plays important roles in many molecular networks when molecular concentrations are in the range of 0.1 muM to 10nM (about 100 to 10 copies in a cell). The chemical master equation provides a fundamental framework for studying these networks, and the time-varying landscape probability distribution over the full microstates, i.e., the combination of copy numbers of molecular species, provide a full characterization of the network dynamics. A complete characterization of the space of the microstates is a prerequisite for obtaining the full landscape probability distribution of a network. However, there are neither closed-form solutions nor algorithms fully describing all microstates for a given molecular network.

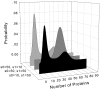
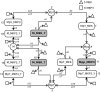
Results: We have developed an algorithm that can exhaustively enumerate the microstates of a molecular network of small copy numbers under the condition that the net gain in newly synthesized molecules is smaller than a predefined limit. We also describe a simple method for computing the exact mean or steady state landscape probability distribution over microstates. We show how the full landscape probability for the gene networks of the self-regulating gene and the toggle-switch in the steady state can be fully characterized. We also give an example using the MAPK cascade network. Data and server will be available at URL: http://scsb.sjtu.edu.cn/statespace.

Conclusion: Our algorithm works for networks of small copy numbers buffered with a finite copy number of net molecules that can be synthesized, regardless of the reaction stoichiometry, and is optimal in both storage and time complexity. The algorithm can also be used to calculate the rates of all transitions between microstates from given reactions and reaction rates. The buffer size is limited by the available memory or disk storage. Our algorithm is applicable to a class of biological networks when the copy numbers of molecules are small and the network is closed, or the network is open but the net gain in newly synthesized molecules does not exceed a predefined buffer capacity. For these networks, our method allows full stochastic characterization of the mean landscape probability distribution, and the steady state when it exists.

Figure 1

The network of a self-regulating gene. (a) The topology of the network. A single copy of the gene in the chromosome encodes a protein transcription factor (TF), which is synthesized at the rate of s₀ or s₁, depending on whether the operator site is bound (state 0) or unbound (state 1). The TF binds the operator site of the gene at a rate of b. It unbinds at a rate of u. The TF is also subject to degradation at a rate of d determined by the degradation machinery. Here the symbol ∅ represent the state of being degraded. (b) The chemical reactions of the five stochastic processes and the corresponding reaction rates.

Figure 2

The steady state landscape probability distributions of a self-regulating gene network. The probability over the number of free protein is plotted. Here this probability is the sum of probabilities for two different gene binding states (bound and unbound) at the same number of free proteins. When the unbound/on state synthesis rate s₁ is greater, the network is self-repressing. When the bound/off synthesis rate s₀ is greater, the network is self-activating. Although the self-repressing (front profile) and the self-activating (back profile) genes have overall similar distributions, the former has a slightly higher probability in producing more free proteins than the latter. When both synthesis rates are equal (middle profile), the network follows a simple birth/death process, with a Gaussian probability distribution.

Figure 3

The network of a toggle switch. (a) The topology of the network and variables representing the reaction rates. Single copies of gene A and gene B in the chromosome each encode a protein product. Two protein monomers can repress the transcription of the other gene. The synthesis of protein product of gene A and B depends on the bound or unbound state of the gene. (b) The chemical reactions of the 8 stochastic processes involved in the toggle-switch network. The reaction rates include s for protein synthesis, d for protein degradation, b for protein-gene binding, and u for protein-gene unbinding.

Figure 4

The steady state probability landscape of a toggle switch. A toggle switch has four different states, corresponding to different binding state of genes A and B. At the condition of small value of u/b, the off/off state is strongly suppressed, and the system exhibits bi-stability.

Figure 5

The MAPK network model according to BioModel (id BIOMD28). The molecular species are labeled with integer numbers. Reactions are labeled with variables representing the corresponding reaction rate, b_i for binding rates, u_i for unbinding rates, and k_i for rates of first order reactions. Solid arrows in this figure represent binding reactions, and empty arrows for unbinding reactions. The parameter values of this model are taken as is from the SBML model. We have: b₁ = 0.005, b₃ = 0.025, b₅ = 0.05, b₇ = 0.005, b₉ = 0.045, b₁₀ = 0.01, b₁₁ = 0.01, b₁₂ = 0.0011, b₁₃ = 0.01, b₁₄ = 0.0018, u_{1,3,5,7,9,10,11,13} = 1, u₂ = 1.08, u₄ = 0.007, u₆ = 0.008, u₈ = 0.45, u₁₂ = 0.086, u₁₄ = 0.14, k₁ = 0.092, k₂ = 0.5, and k₃ = 0.47.

Figure 6

Sizes of state spaces for a model of the MAPK cascades under the initial condition of 1 to 20 copies of each of the 16 species in turn and 0 in all other species. Altogether the size of state space for 16 × 20 = 320 initial conditions are shown here.

Figure 7

The marginal landscape probability distribution of different copy numbers of molecular species in the MAPK network in steady state. (a) Marginal probability distribution of the combination of the number of unphosphorylated ERK (M) and uniphosphorylated ERK (Mp, including both MpY and MpT), regardless of the copy numbers of all other molecular species; (b) Marginal probability distribution of the combination of the copy numbers of unphosphorylated ERK (M) and dual-phosphorylated ERK (Mpp); (c) Marginal probability distribution of the combination of the copy numbers of uniphosphorylated Mp and dual phosphorylated Mpp.