Discrete state model and accurate estimation of loop entropy of RNA secondary structures

Abstract

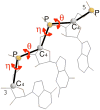
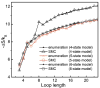
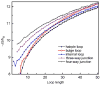
Conformational entropy makes important contribution to the stability and folding of RNA molecule, but it is challenging to either measure or compute conformational entropy associated with long loops. We develop optimized discrete k-state models of RNA backbone based on known RNA structures for computing entropy of loops, which are modeled as self-avoiding walks. To estimate entropy of hairpin, bulge, internal loop, and multibranch loop of long length (up to 50), we develop an efficient sampling method based on the sequential Monte Carlo principle. Our method considers excluded volume effect. It is general and can be applied to calculating entropy of loops with longer length and arbitrary complexity. For loops of short length, our results are in good agreement with a recent theoretical model and experimental measurement. For long loops, our estimated entropy of hairpin loops is in excellent agreement with the Jacobson-Stockmayer extrapolation model. However, for bulge loops and more complex secondary structures such as internal and multibranch loops, we find that the Jacobson-Stockmayer extrapolation model has large errors. Based on estimated entropy, we have developed empirical formulae for accurate calculation of entropy of long loops in different secondary structures. Our study on the effect of asymmetric size of loops suggest that loop entropy of internal loops is largely determined by the total loop length, and is only marginally affected by the asymmetric size of the two loops. Our finding suggests that the significant asymmetric effects of loop length in internal loops measured by experiments are likely to be partially enthalpic. Our method can be applied to develop improved energy parameters important for studying RNA stability and folding, and for predicting RNA secondary and tertiary structures. The discrete model and the program used to calculate loop entropy can be downloaded at http://gila.bioengr.uic.edu/resources/RNA.html.

FIG. 1

(Color online) A schematic diagram showing RNA secondary structures of hairpin, bulge, internal, and multibranch loops.

FIG. 2

(Color online) The virtual bond representation of RNA backbone. The torsional angles θ and η are calculated and used in the analysis of backbone rotamers.

FIG. 3

(Color online) The set of (θ,η) angle pairs of clusters in RNA molecules and the centers of k-clusters calculated by the k-mean clustering method. The centers are marked by stars. (a), (b), and (c) are for k=4, 5, and 6 clusters, respectively. (d) shows the distribution of Silhouette value calculated for the 4-state clustering procedure.

FIG. 4

The flowchart showing the SMC sampling algorithm.

FIG. 5

(Color online) Comparison of loop entropies calculated by exhaustive enumeration and estimated by sequential Monte Carlo (SMC) sampling method using the 4-state, 5-state, and 6-state model. They are essentially indistinguishable, suggesting that our sampling method works well.

FIG. 6

The calculated entropies of hairpin, bulge and internal loops and the corresponding experimental values. The model used in calculation is the 6-state model. All the three figures are plotted with the same scale, which is also the same with that used in Ref. to facilitate comparison with the previous theoretical model.

FIG. 7

Comparison of the hairpin loop entropies calculated by 5- and 6-state models and the extrapolated values (note that the values at n≤9 are determined by experiments). The curve calculated by 6-state model is smoother than that by 5-state model because the calculation are repeated many times to ensure the relative standard error is less than 1%.

FIG. 8

Comparison of the bulge loop entropies calculated by 5- and 6-state models and the extrapolated values (the values for n≤5 are determined by experiments). The entropy calculated by 4-state model is not shown because it is significantly smaller than the extrapolated value, similar to the case of hairpin loop. The fitted curve using Eq. (3) is also shown in (b).

FIG. 9

Comparison of the internal loop entropies calculated by 5- and 6-state models and the extrapolated values. The values for n≤6 are determined by experiments. The fitted curve using the empirical model of Eq. (4) is shown in (b).

FIG. 10

Comparison of the three-way multibranch loop entropies calculated by 5- and 6-state models and the values calculated by the empirical model (see the text). The fitted curve using the empirical model Eq. (5) is shown in (b).

FIG. 11

(Color online) Comparison of the calculated entropies of hairpin, bulge, internal, three-way, and four-way multibranch loops. It can be seen clearly that the slope of the entropy curve decreases as the number of helices increases.

FIG. 12

(Color online) The loop entropy as a function of size asymmetry |n1−n2|, calculated for all combinations of loop length of internal loops of lengths n=n1+n2≤ 50. The entropy of loops with odd number of n>11 are not shown in the interest of clear presentation. The data points connected by a line have the same loop length n.