Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2007:2007:92780.
doi: 10.1155/2007/92780.

The Mathematical Foundations of 3D Compton Scatter Emission Imaging

T T Truong  1 , M K Nguyen, H Zaidi
Affiliations

The Mathematical Foundations of 3D Compton Scatter Emission Imaging

T T Truong et al. Int J Biomed Imaging. 2007.

Abstract

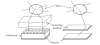
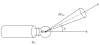
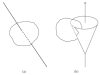
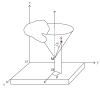
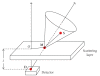
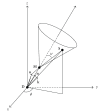
The mathematical principles of tomographic imaging using detected (unscattered) X- or gamma-rays are based on the two-dimensional Radon transform and many of its variants. In this paper, we show that two new generalizations, called conical Radon transforms, are related to three-dimensional imaging processes based on detected Compton scattered radiation. The first class of conical Radon transform has been introduced recently to support imaging principles of collimated detector systems. The second class is new and is closely related to the Compton camera imaging principles and invertible under special conditions. As they are poised to play a major role in future designs of biomedical imaging systems, we present an account of their most important properties which may be relevant for active researchers in the field.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Two imaging modalities using scattered radiation with and without collimation.
Figure 2
Figure 2
Compton scattering differential cross-section.
Figure 3
Figure 3
Illustration of linear and conical projections.
Figure 4
Figure 4
𝒞 1-cone and 𝒞 1-conical Radon transform definition.
Figure 5
Figure 5
Principle of a Compton camera.
Figure 6
Figure 6
𝒞 2-cone and 𝒞 2-conical Radon transform definition.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Natterer F. The Mathematics of Computerized Tomography. Philadelphia, Pa, USA: SIAM; 2001. (Classics in Applied Mathematics).
    1. Cormack AM. My connection with the Radon transform. In: Gindikin S, Michor P, editors. 75 Years of Radon Transform. Vol. 4. Boston, Mass, USA: International Press; 1994. pp. 32–35. (Conference Proceedings and Lecture Notes in Mathematical Physics).
    1. Cormack AM. Representation of a function by its line integrals, with some radiological applications. Journal of Applied Physics. 1963;34(9):2722–2727.
    1. Cormack AM. Representation of a Function by Its Line Integrals, with Some Radiological Applications. II. Journal of Applied Physics. 1964;35(10):2908–2913.
    1. Radon J. Über die Bestimmung von Funktionnen durch ihre Integralwerte längs gewisser Mannigfaltikeiten. Berichte über die Verhandlungen der Säschsischen Akademie der Wissenschaften zu Leipzig, Mathematisch-Naturwissenschaftliche Klasse. 1917;69:262–277.