An optimized blockwise nonlocal means denoising filter for 3-D magnetic resonance images

Abstract

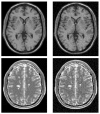
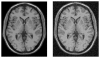
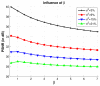
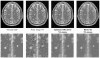
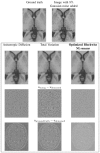
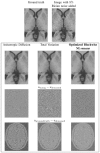
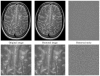
A critical issue in image restoration is the problem of noise removal while keeping the integrity of relevant image information. Denoising is a crucial step to increase image quality and to improve the performance of all the tasks needed for quantitative imaging analysis. The method proposed in this paper is based on a 3-D optimized blockwise version of the nonlocal (NL)-means filter (Buades, et al., 2005). The NL-means filter uses the redundancy of information in the image under study to remove the noise. The performance of the NL-means filter has been already demonstrated for 2-D images, but reducing the computational burden is a critical aspect to extend the method to 3-D images. To overcome this problem, we propose improvements to reduce the computational complexity. These different improvements allow to drastically divide the computational time while preserving the performances of the NL-means filter. A fully automated and optimized version of the NL-means filter is then presented. Our contributions to the NL-means filter are: 1) an automatic tuning of the smoothing parameter; 2) a selection of the most relevant voxels; 3) a blockwise implementation; and 4) a parallelized computation. Quantitative validation was carried out on synthetic datasets generated with BrainWeb (Collins, et al., 1998). The results show that our optimized NL-means filter outperforms the classical implementation of the NL-means filter, as well as two other classical denoising methods [anisotropic diffusion (Perona and Malik, 1990)] and total variation minimization process (Rudin, et al., 1992) in terms of accuracy (measured by the peak signal-to-noise ratio) with low computation time. Finally, qualitative results on real data are presented .

Fig. 1

Left: Classical voxelwise NL-means filter: 2D illustration of the NL-means principle. The restored value of voxel x_i (in red) is the weighted average of all intensities of voxels x_j in the search volume V_i, based on the similarity of their intensity neighborhoods u(N_i) and u(N_j). In this example, we set d = 1 and M = 8. Right: Blockwise NL-means filter: 2D illustration of the blockwise NL-means principle. The restored value of the block B_ik is the weighted average of all the blocks B_j in the search volume V_ik. In this example, we set α = 1 and M = 8.

Fig. 2

Left: noisy image with 9 % of Gaussian noise (see Section IV). Center: map of the mean of u(N_i) denoted $\overline{\mathbf{u}(N_i)}$. Right map of the variance of u(N_i) denoted Var(u(N_i)). In these examples, we set N_i = 5 × 5 × 5 voxels.

Fig. 3. Blockwise NL-means Filter

For each block B_ikcentered on voxel x_ik, a NL-means like restoration is performed from blocks B_j. In this way, for a voxel x_i included in several blocks, several estimations are obtained. The restored value of voxel x_i is the average of the different estimations stored in vector A_i. In this example α = 1, n = 2 and |A_i| = 3.

Fig. 4. Synthetic data used for validation with Gaussian Nnoise

Example of the Brainweb Database. Top: T1-w images without any noise (left), and corrupted with a white Gaussian noise at 9% (right). Bottom: T2-w images with MS lesions without noise (left), and corrupted with a white Gaussian noise at 9% (right).

Fig. 5. Synthetic data used for validation with Rician noise

Example of the Brainweb Database. T1-w images without any noise (left), and corrupted with a Rician noise at 9% (right).

Fig. 6. Calibration of the smoothing parameter

h: Influence of the smoothing parameter 2βσ̂²|N_i| on the PSNR, according to β and for several levels of noise. For low levels of noise the best value of β is close to 0.5. For high levels of noise this value is 1. The default value of β is set to 1, thus the estimation of h is h² = 2σ̂². These results are obtained with σ̂² = 3.42% at 3%, σ̂² = 7.93% at 9%, σ̂² = 12.72% at 15% and σ̂² = 17.44% at 21%.

Fig. 7. Influence of the size |V_i| = (2M + 1)³ and |N_i| = (2d + 1)³ for denoising

Influence of the size of the search volume and the size of the neighborhood on the PSNR, for several levels of noise. Left: Variation of the size M of the search volume V_i for d = 1. Right: Variation of the size d of the neighborhood N_i for M = 5. These results show that the limit M = 5 prevents useless computation. Moreover, increasing d degrades and drastically slows down the algorithm.

Fig. 8. Influence of the limits of the voxels selection

Influence of the limits μ₁ and ${\sigma }_1^2$ on the PSNR, for several level of noise. Left: ${\sigma }_1^2=0.5$, while μ₁ varies with γ. A restrictive selection based on the mean (low values of γ) increases the PSNR. The optimal limits are obtained for μ₁ = 0.95. Right: μ₁ = 0.95 and ${\sigma }_1^2$ varies accordingly to γ. A too restrictive selection (low values of γ) degrades the PSNR. In addition, a too permissive selection (high values of γ) does not increase the PSNR while concurrently increasing uselessly the computational burden. A good compromise is found by fixing ${\sigma }_1^2=0.5$.

Fig. 9. Impact of the blockwise implementation and voxels selection

Comparison of the different implementations of the NL-means filter, with α = 1. Left: on T1-w images. For the Optimized Blockwise NL-means filter, as for the Optimized NL-means filter, the selection of voxels/blocks in the search volume improves the quality of denoising and decreases the computational burden (see Tab. II). The reduction of computational time brought by the blockwise approach needs to be balanced with a slight decrease in quality of denoising. Right: on T2-w images with MS lesions. The same conclusions can be drawn for this kind of images. These results suggest that the parameters tuning determined experimentally on T1-w images are not T1-specific.

Fig. 10. Comparison of the optimized and non-optimized blockwise NL-means on T2-w images

NL-means restoration of T2-w Brainweb data with MS lesions. From left to right: “Ground truth”, noised image at 9% of Gaussian noise, restored images by the Optimized Blockwise NL-means filter and by the Blockwise NL-means filter. The Optimized Blockwise NL-means filter preserves efficiently the contours of the MS lesions.

Fig. 11

Result for AD filter and TV minimization on phantom images with Gaussian noise at 9%. For AD filter K varies from 0.05 to 1 with step of 0.05 and the number of iterations varies from 1 to 10. For TV minimization λ varies from 0.01 to 1 with step of 0.01 and the number of iterations varies from 1 to 10

Fig. 12. Comparison between Anisotropic Diffusion, Total Variation and Optimized Blockwise NL-means denoising

the PSNR values and histograms for different denoising methods on BrainWeb at 9% of Gaussian noise. Left: the PSNR experiment shows that the Optimized Blockwise NL-means filter outperforms the well-established Total Variation minimization process and the Anisotropic Diffusion approach. Right: Contrary to others methods, the NL-means based restoration clearly distinguishes the three main peaks representing the white matter, the gray matter and the cerebrospinal fluid. The sharpness of the peaks shows how the Optimized Blockwise NL-means filter increases the contrast between denoised biological structures.

Fig. 13. Comparison with Anisotropic Diffusion, Total Variation and NL-means denoising on synthetic T1-w images

Top: zooms on T1-w BrainWeb images. Left: the “ground truth”. Right: the noisy images with 9% of Gaussian noise. Middle: the results of restoration obtained with the different methods and the images of the removed noise (i.e. the difference (centered on 128) between the noisy image and the denoised image. Bottom: the difference (centered on 128) between the denoised image and the ground truth. Left: Anisotropic Diffusion denoising. Left: Anisotropic Diffusion denoising. Middle: Total Variation minimization process. Right: Optimized Blockwise NL-means filter. The NL-means based restoration better preserves the anatomical structure in the image while efficiently removing the noise as it can be seen in the image of removed noise.

Fig. 14. Comparison with Anisotropic Diffusion, Total Variation and NL-means denoising on synthetic T1-w images

Top: zooms on T1-w BrainWeb images. Left: the “ground truth”. Right: the noisy images with 21% of Gaussian noise. Middle: the results of restoration obtained with the different methods and the images of the removed noise (i.e. the difference (centered on 128) between the noisy image and the denoised image. Bottom: the difference (centered on 128) between the denoised image and the ground truth. Left: Anisotropic Diffusion denoising. Middle: Total Variation minimization process. Right: Optimized Blockwise NL-means filter.

Fig. 15. Comparison with Anisotropic Diffusion, Total Variation and Optimized Blockwise NL-means denoising

PSNR values and histograms for different denoising methods on BrainWeb at 9% of Rician noise. Left: the PSNR study shows that the Optimized Blockwise NL-means filter outperforms the well-established Total Variation minimization process and the Anisotropic Diffusion approach. Right: When the histograms are compared low values of intensity (< 20) are incorrectly restored for all the filters; the Gaussian approximation is not appropriate in that case. Nevertheless, it seems the underlying assumption is well suited to high values (> 60). Contrary to others methods, the NL-means based restoration clearly emphasizes the three main peaks representing the white matter, the gray matter and the cerebrospinal fluid. The sharpness of the peaks shows how the Optimized Blockwise NL-means filter increases the contrast between denoised biological structures.

Fig. 16. Comparison with Anisotropic Diffusion, Total Variation and NL-means denoising on synthetic T1-w images

Top: zooms on T1-w BrainWeb images. Left: the “ground truth”. Right: the noisy images with 9% of Rician noise. Middle: the results of restoration obtained with the different methods and the images of the removed noise (i.e. the difference (centered on 128) between the noisy image and the denoised image. Bottom: the “Method Noise” which is the difference (centered on 128) between the denoised image and the ground truth. Left: Anisotropic Diffusion denoising. Middle: Total Variation minimization process. Right: Optimized Blockwise NL-means filter. The NL-means based restoration better preserves the anatomical structure in the image while efficiently removing the noise, it can be seen in the image of removed noise.

Fig. 17

Result for AD filter and TV minimization on phantom images with 9% of Rician noise. For AD filter K varies from 0.05 to 1 with step of 0.05 and the number of iterations varies from 1 to 10. For TV minimization λ varies from 0.01 to 1 with step of 0.01 and the number of iterations varies from 1 to 10.

Fig. 18. NL-means filter on a real T1-w MRI

Fully-automatic restoration obtained with the Optimized Blockwise NL-means filter on a 3 Tesla T1-w MRI data of 256³ voxels in less than 3 minutes on a Intel(R) Pentium(R) D CPU 3.40GHz with 2Go of RAM. From left to right: Original image, denoised image, and difference image with gray values centered on 128. The whole image is shown on top, and a detail is displayed on bottom.

Fig. 19. NL-means filter on a real T2-w MRI with MS

Fully-automatic restoration obtained with the Optimized Blockwise NL-means filter on a 1.5T T2-w MRI data with MS lesions of 512 × 512 × 28 voxels in less than 2 minute on a Intel(R) Pentium(R) D CPU 3.40GHz with 2Go of RAM. From left to right: Original image, denoised image, and difference image with gray values centered on 128. The whole image is shown on top, and a detail is exposed on bottom.