Accelerating QM/MM free energy calculations: representing the surroundings by an updated mean charge distribution

Abstract

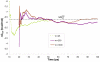
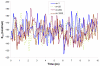
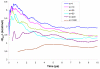
Reliable studies of enzymatic reactions by combined quantum mechanical/molecular mechanics (QM(ai)/MM) approaches with an ab initio description of the quantum region presents a major challenge to computational chemists. The main problem is the need for very large computer time to evaluate the QM energy, which in turn makes it extremely challenging to perform proper configurational sampling. One of the most obvious options for accelerating QM/MM simulations is the use of an average solvent potential. In fact, the idea of using an average solvent potential is rather obvious and has implicitly been used in Langevin dipole/QM calculations. However, in the case of explicit solvent models the practical implementations are more challenging, and the accuracy of the averaging approach has not been validated. The present study introduces the average effect of the fluctuating solvent charges by using equivalent charge distributions, which are updated every m steps. Several models are evaluated in terms of the resulting accuracy and efficiency. The most effective model divides the system into an inner region with N explicit solvent atoms and an external region with two effective charges. Different models are considered in terms of the division of the solvent system and the update frequency. Another key element of our approach is the use of the free energy perturbation (FEP) and/or linear response approximation treatments that guarantees the evaluation of the rigorous solvation free energy. Special attention is paid to the convergence of the calculated solvation free energies and the corresponding solute polarization. The performance of the method is examined by evaluating the solvation of a water molecule and a formate ion in water and also the dipole moment of water in water solution. Remarkably, it is found that different averaging procedures eventually converge to the same value but some protocols provide optimal ways of obtaining the final QM(ai)/MM converged results. The current method can provide computational time saving of 1000 for properly converging simulations relative to calculations that evaluate the QM(ai)/MM energy every time step. A specialized version of our approach that starts with a classical FEP charging and then evaluates the free energy of moving from the classical potential to the QM/MM potential appears to be particularly effective. This approach should provide a very powerful tool for QM(ai)/MM evaluation of solvation free energies in aqueous solutions and proteins.

Figure 1

Energy scheme. $\Delta G_{\mathit{sol}}\left(Q_{\mathit{PCM}}^0\right)$ is calculated by the classical adiabatic charging approach.

Figure 2

A schematic representation of the averaging of the solvent potential over m steps of a MD simulation.

Figure 3

Different models for the evaluation of the average solvent charges: model M1 (a) involves an averaging of the explicit solvent molecules; models M2 and M3 (b) average the explicit molecules in region (I) while representing the average potential of the molecule in region II by two charges; model M4 (c) represents the solvent effect by two charges.

Figure 4

Convergence of the average interaction energy during 10ps simulations (m=1) using different models of solvent representation.

Figure 5

Interaction energy during 10ps simulations of water molecule in water using model M2. The charge on the solute atoms were updated every m^th step.

Figure 6

Average solute-solvent interaction energy during 10 ps simulations of a water molecule in water solution (model M2).

Figure 7

Average solute polarization energy during 10 ps simulations of water molecule in a water solution (model M2).

Figure 8

Fourier transform of the fluctuating interaction energy as a function of the simulation length and the value of m obtained in simulation of water molecule in water using model M2.

Figure 9

Schematic convergence.

Figure 10

Average dipole moment of water molecule in water along a 10 ps simulation using model M2.

Figure 11

Free energy of solvation of water along 50 and 100 ps simulation of water molecule in water solution.

Figure 12

Interaction energy along 10ps simulations of HCOO⁻ in water using model M2. Charge on the solute atoms updated every m^th step.

Figure 13

Average solute-solvent interaction energy along 10 ps simulation of HCOO⁻ solvated by water (model M2).

Figure 14

Average solute polarization energy along 10 ps simulation of HCOO⁻ ion in water solution (model M2).

Figure 15

Free energy of solvation of the formate ion along 50 and 100 ps simulation. The calculations were performed using Eq. (4) and corrected by adding the difference between the ΔG_sol of Eq. (7) and ΔG_sol of Eq. (4).