A comparison of plotless density estimators using Monte Carlo simulation on totally enumerated field data sets

Abstract

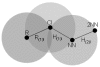
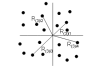
Background: Plotless density estimators are those that are based on distance measures rather than counts per unit area (quadrats or plots) to estimate the density of some usually stationary event, e.g. burrow openings, damage to plant stems, etc. These estimators typically use distance measures between events and from random points to events to derive an estimate of density. The error and bias of these estimators for the various spatial patterns found in nature have been examined using simulated populations only. In this study we investigated eight plotless density estimators to determine which were robust across a wide range of data sets from fully mapped field sites. They covered a wide range of situations including animal damage to rice and corn, nest locations, active rodent burrows and distribution of plants. Monte Carlo simulations were applied to sample the data sets, and in all cases the error of the estimate (measured as relative root mean square error) was reduced with increasing sample size. The method of calculation and ease of use in the field were also used to judge the usefulness of the estimator. Estimators were evaluated in their original published forms, although the variable area transect (VAT) and ordered distance methods have been the subjects of optimization studies.

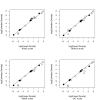
Results: An estimator that was a compound of three basic distance estimators was found to be robust across all spatial patterns for sample sizes of 25 or greater. The same field methodology can be used either with the basic distance formula or the formula used with the Kendall-Moran estimator in which case a reduction in error may be gained for sample sizes less than 25, however, there is no improvement for larger sample sizes. The variable area transect (VAT) method performed moderately well, is easy to use in the field, and its calculations easy to undertake.

Conclusion: Plotless density estimators can provide an estimate of density in situations where it would not be practical to layout a plot or quadrat and can in many cases reduce the workload in the field.

Figure 1

Schematic representation of how KM2P and BDAV3 are implemented in the field. Shading shows the search area less intersection used in the calculation of KM2P. R – the random sample point CI – closest individual; NN – nearest neighbor; 2NN – second nearest neighbor, R_(1)i = the distance from the i^th sample point to the CI; H_(1)i = the distance from the i^th CI to its NN; H_(2)i = the distance from the NN at the i^th random point.

Figure 2

Schematic representation of how AO3Q is implemented in the field. The order of the quadrants is arbitrary. In practice much time is spent deciding which is the third closest individual and into which quadrant an individual lies. R_(3)ij = the distance from the i^th sample point to the third CI for the j^th quadrant.

Figure 3

Correlation between mean density estimate against known density for all data sets. Line shows complete agreement between known and estimated density. Spearman's correlation coefficient shown in parentheses. Symbols denote spatial pattern of data set: Uniform – filled circle, Poisson – filled triangle, Clumped – open circle.

Figure 4

Examples of diversity of spatial patterns found. (a) uniform distribution of pocket gopher burrows; (b) aggregated nesting pattern of waterfowl; (c) random pattern of rodent damage in rice; (d) highly clumped damage within a cornfield.

Figure 5

Subsets within the highly clumped Corn 2 data set showing random and uniform patterns, see Table 6.