Estimation of pairwise identity by descent from dense genetic marker data in a population sample of haplotypes
- PMID: 18430938
- PMCID: PMC2323802
- DOI: 10.1534/genetics.107.084624
Estimation of pairwise identity by descent from dense genetic marker data in a population sample of haplotypes
Abstract
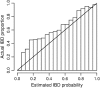
I present a new approach for calculating probabilities of identity by descent for pairs of haplotypes. The approach is based on a joint hidden Markov model for haplotype frequencies and identity by descent (IBD). This model allows for linkage disequilibrium, and the method can be applied to very dense marker data. The method has high power for detecting IBD tracts of genetic length of 1 cM, with the use of sufficiently dense markers. This enables detection of pairwise IBD between haplotypes from individuals whose most recent common ancestor lived up to 50 generations ago.
Figures



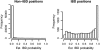
References
-
- Baum, L. E., 1972. An inequality and associated maximization technique in statistical estimation for probabilistic functions on Markov processes, pp. 1–8 in Inequalities. III. Proceedings of the Third Symposium on Inequalities. Academic Press, New York.
-
- Beckmann, L., D. C. Thomas, C. Fischer and J. Chang-Claude, 2005. Haplotype sharing analysis using Mantel statistics. Hum. Hered. 59 67–78. - PubMed
-
- Browning, B. L., and S. R. Browning, 2007. Efficient multilocus association mapping for whole genome association studies using localized haplotype clustering. Genet. Epidemiol. 31 365–375. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

