3D wavelet subbands mixing for image denoising

Abstract

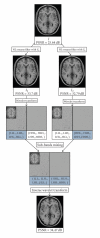
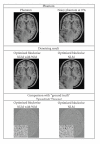
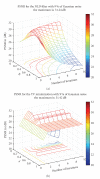
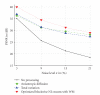
A critical issue in image restoration is the problem of noise removal while keeping the integrity of relevant image information. The method proposed in this paper is a fully automatic 3D blockwise version of the nonlocal (NL) means filter with wavelet subbands mixing. The proposed wavelet subbands mixing is based on a multiresolution approach for improving the quality of image denoising filter. Quantitative validation was carried out on synthetic datasets generated with the BrainWeb simulator. The results show that our NL-means filter with wavelet subbands mixing outperforms the classical implementation of the NL-means filter in terms of denoising quality and computation time. Comparison with wellestablished methods, such as nonlinear diffusion filter and total variation minimization, shows that the proposed NL-means filter produces better denoising results. Finally, qualitative results on real data are presented.

Figure 1

(a) Usual voxelwise NL-means filter: 2D illustration of the NL-means principle. The restored value of voxel x _i (in red) is the weighted average of all intensities of voxels x _j in the search volume V _i, based on the similarity of their intensity neighborhoods u(N _i) and u(N _j). In this example, we set d = 1 and M = 8. (b) Blockwise NL-means filter: 2D illustration of the blockwise NL-means principle. The restored value of the block B _ik is the weighted average of all the blocks B _j in the search volume V _ik. In this example, we set α = 1 and M = 8.

Figure 2

Blockwise NL-means filter. For each block B _ik centered on voxel x _ik, an NL-means-like restoration is performed from blocks B _j. In this way, for a voxel x _i included in several blocks, several estimations are obtained. The restored value of voxel x _i is the average of the different estimations stored in vector A _i. In this example, α = 1, n = 2, and |A _i| = 3..

Figure 3

Workflow. First, the noisy image I is denoised with two sets of filtering parameters S _u and S _o. Then, I _u and I _o are decomposed into low- and high-frequency subbands by 3D DWT. The four lowest frequency subbands of I _u (i.e., LLL₁, LLH₁, LHL₁, and HLL₁) are mixed with the four highest-frequency subbands of I _o (i.e., LHH₁, HLH₁, HHL₁, and HHH₁). Finally, the result image is obtained by inverse 3D DWT of the selected subbands.

Figure 4

Influence of the filtering parameter $2\beta {\widehat{\sigma }}^2$ on the PSNR according to β and for several levels of noise. These results are obtained with the optimized blockwise NL-means filter on the T1-w phantom MRI and account for the error in the estimation of σ.

Figure 5

Comparison of the different NL-means filters on T1-w phantom MRI and T2-w phantom MRI with MS.

Figure 6

Fully automatic restoration obtained with the optimized blockwise NL-means with wavelet mixing filter in 3 minutes on a DualCore Intel(R) Pentium(R) D CPU 3.40 GHz. The image is a T2-w phantom MRI with MS of 181 × 217 × 181 voxels and 9% of noise.

Figure 7

Top. Phantom and phantom noisy with 9%. Middle. The denoising result obtained with the optimized blockwise NLM with WM filter and the optimized blockwise NLM filter. Bottom. The image of difference between the phantom and the denoising result (i.e., u _groundtruth-u _denoised). The contrast of the zooms have been artificially increased. Visually, less structures have been removed with the optimized blockwise NLM with WM filter.

Figure 8

Result for the NLD filter and the TV minimization on phantom images with Gaussian noise at 9%. For the NLD filter, K varied from 0.05 to 1 with a step of 0.05 and the number of iterations varied from 1 to 10. For the TV minimization, λ varied from 0.01 to 1 with a step of 0.01 and the number of iterations varied from 1 to 10.

Figure 9

Comparison between nonlinear diffusion, total variation, and optimized blockwise NL-means with wavelet mixing denoising. The PSNR experiments show that the optimized blockwise NL-means with wavelet mixing filter significantly outperforms the well-established total variation minimization 𝔹 ⁵ process and the nonlinear diffusion approach.

Figure 10

Comparison between nonlinear diffusion, total variation, and our optimized blockwise NL-means with wavelet mixing denoising on synthetic T1-w images. Top. Zooms on T1-w BrainWeb images. Left. The “ground truth”. Right. The noisy images with 9% of Gaussian noise. Middle. The results of restoration obtained with the different methods and the images of the removed noise (i.e., the difference (centered on 128) between the noisy image and the denoised image. Bottom. The difference (centered on 128) between the denoised image and the ground truth. Left. Nonlinear diffusion denoising. Left. Nonlinear diffusion denoising. Middle. Total variation minimization process. Right. Optimized Blockwise NL-means with WM filter. The NL-means-based restoration better preserves the anatomical structure in the image while efficiently removing the noise as it can be seen in the image of removed noise.

Figure 11

Fully automatic restoration obtained with the optimized blockwise NL-means with wavelet mixing filter on a 3 Tesla T1-w MRI data of 256³ voxels in less than 4 minutes on a DualCore Intel(R) Pentium(R) D CPU 3.40 GHz.